Three simple harmonic motions in the same direction having the same amplitude and same period are superposed. If each differ in phase from the next by 45∘, then Solution in Gujrati
(a)resultant amplitude is (1+√2)a
(b)phase of the resultant motion relative to the first is 90∘
(c)energy associated with the resultaing motion is (3+2√2) time the energy associated with any single motion
(d)resulting motion is not simple harmonic
The correct Answer is:A, C
From susperposition principal
y=y1+y2+y3
=asinωt+asin(ωt+45∘)+asin(ωt+90∘)
=a[sinωt+sin(ωt+90∘)]+asin(ωt+45∘)
=2asin(ωt+45∘)cos45∘+asin(ωt+45∘)
=(√2+1)asin(ωt+45∘)=Asin(ωt+45∘)
Therefore, resultant motion is simple harmonic of amplitude. A=(√2+1) and which differ in phase by 45∘ relative to the first.
∴EresultantEsingle=(Aa)2=(√2+1)2=(3+2√2)
∴Eresultant=(3+2√2)Esingle
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Paragraph
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Subjective
30 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]
12 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
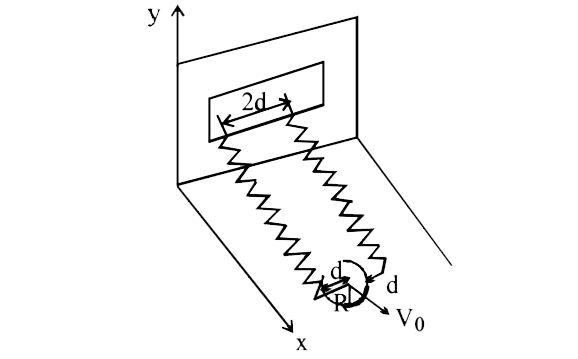
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionTwo masses m1 and m2 concute a high spring of natural length l0 is compressed completely and tied by a string. This system while conving with a velocity v0 along +ve x-axis pass thorugh the origin at t=0, at this position the string sanps, Position of mass m1 at time t is given by the equation x1t=v0(A/1−cosωt). Calculate (i) position of the particle m2 as a funcation of time, (ii) l0 in terms of A.
View SolutionA particle of mass (m) is executing oscillations about the origin on the x axis. Its potential energy is V(x)=k|x|3 where k is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionThree simple harmonic motions of equal amplitudes A and equal time periods in the same direction combine. The phase of the second motion is 60∘ ahead of the first and the phase of the third motion is 60∘ ahead of the second. Find the amplitude of the resultant motion.
View SolutionThree simle harmionic motions in the same direction having the same amplitude (a) and same period are superposed. If each differs in phase from the next by 45∘, then.
View SolutionThree simple harmonic motion of equal amplitudes A and equal time periods in the same direction combine. The phase of the second motion is 60∘ ahead of the first and the phase of the third motion is 60∘ ahead of the second. Find the amplitude of the resultant motion.
View SolutionA particle is subjected to two simple harmonic motion in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions. Find the phase difference between the individual motions.
View SolutionThree simple harmonic motions in the same direction each of amplitude a and periodic time T , are superposed. The first and second and the second and third differ in phase from each other by (pi)/(4) , with the first and third not being identical . Then.
View SolutionThree simple harmonic motions in the same direction having each of amplitude "a" and the same period are superposed. If each differs in phase from the next by π/4 then
View SolutionThree simple harmonic motions in the same direction having same amplitude and the same period are superposed. If each differs in phase from the next by lambda//2 then which of the following is wron. ( i ) Resultant amplitude is (sqrt(2)+1) a ( ii ) Phase of resultant motion relative to first is 90^(@) ( iii ) The energy associated with the resulting motion is 3 times the energy associated with any single motion
View SolutionWhen two simple harmonic motions of same periods, same amplitude, having phase difference of 3π/2, and at right angles to each other are super imposed, the resultant wave from is a
View SolutionThree simple harmonic motions in the same direction having the same amplitude and same period are superposed. If each differ in phase from the next by 45∘, then
View Solutionसमान आयाम a तथा समान आवर्तकाल वाली तीन सरल आवर्त गतियाँ एक ही दिशा में अधिरोपित की जाती है। यदि प्रत्येक गति का अगली गति से कलांतर 45∘ है, तब
View Solution
