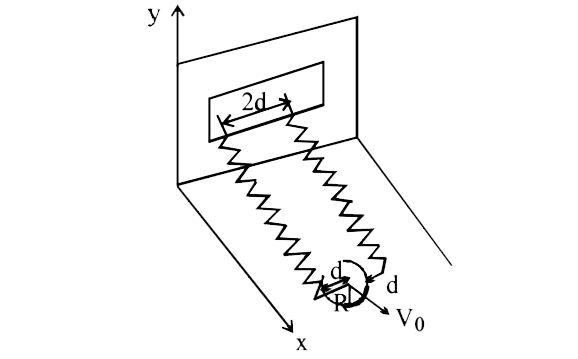
Two masses m1 and m2 concute a high spring of natural length l0 is compressed completely and tied by a string. This system while conving with a velocity v0 along +ve x-axis pass thorugh the origin at t=0, at this position the string sanps, Position of mass m1 at time t is given by the equation x1t=v0(A/1−cosωt). Calculate (i) position of the particle m2 as a funcation of time, (ii) l0 in terms of A.Solution in Gujrati
The correct Answer is:(i) v0t+Am1m2(1−cosωt) , (ii) (m1m2+1)A
(i) Two massse m1 and m2 are connected by a spring of length l0. The spring is in compressed position. It is held in this position by a string. When the string snaps, the spring force is brought into operation. The spring force is an internal force w.r.t masses-spring system. No external force is applied on the system. The velocity of centre of mass will not change.
Velocity of centre of mass =v0
∴ Location/x -coordinate of centre of mass of time
t=v0t
∴¯v=m1x1+m2x2m1+m2
⇒v0t=m1[v0t−A(1−cosωt)]+m2x2m1+m2
⇒(m1+m2)v0t=m1[v0t−A(1−cosωt)]+m2x2)
⇒m1v0t+m2v0t=m1v.0t−m1A(1−cosωt)]+m2x2
⇒m2x2=m2v0t+m1A(1−cosωt)
⇒x2=v0t+m1Am2(1−cosωt)......(i)
To express l0 in terms of A.
∴x1=v0t−A(1−cosωt)∴dx1dt2=−Aω2sinωt
∴d2x2dt2=−Aω2cosωt........(ii)
x1 is displacement of m1 at time t.
∴d2x1dt2= acceleration of m1 at time t.
When the spring attains its natural length l0, then acceleration is zero and (x2−x1)=l0)
∴x2x1=l0 , Put x2 from (i)
⇒[v0t+m1Am2(1−cosωt)]−[v0t−A(1−cosωt)]=l0
⇒l0=(m1m2+1)A(1−cosωt)
When d2x1dt2=0,cosωt=0 from (ii).
∴l0=(m1m2+1)A.
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Example3videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - X Rays : Solved Example2videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Paragraph3videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A hydrogen like atom with atomic number Z is in an excited state of quantum number 2n. It can emit a maximum energy photon of 204 eV. If it makes a transition ot quantum state n, a photon of energy 40.8 eV is emitted. Find n, Z and the ground state energy (in eV) of this atom. Also calculate the minimum energy (in eV) that can be emitted by this atom during de-excitation. Ground state energy of hydrogen atom is – 13. 6 eV.
04:36View SolutionWhen X-rays if wavelength 0.5Å pass through 10mm thick Al sheet than their intensity is reduced to one sixth . Find the absorption coefficient for Aluminium.
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
01:35View SolutionChoose the correct statement:
View SolutionTwo blocks of mass m1 and m2 (m1<m2) are connected with an ideal spring on a smooth horizontal surface as shown in figure. At t = 0 m1 is at rest and m2 is given a velocity v towards right. At this moment, spring is in its natural length. Then choose the correct alternative :
 02:51View Solution
02:51View SolutionTwo masses m_(1) and m_(2) connected by a light spring of natural length l_(0) is compressed completely and tied by a string. This system while moving with a velocity v_(0) along +ve x -axis pass through the origin at t=0 . At this position the string snaps. Postion of mass m_(1) at time t is given by the equation. x_(1) (t)=v_(0)t-A(1-cosomegat) calculate : (a) Position of the particle m_(2) as a function of time. (b) l_(0) in terms of A .
03:12View SolutionTwo particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time
 05:56View Solution
05:56View SolutionTwo bodies having masses m_(1) and m_(2) and velocities v_(1) and v_(2) colide and form a composite system. If m_(1)v_(1) + m_(2)v_(2) = 0(m_(1) ne m_(2) . The velocity of composite system will be
View SolutionTwo masses m1 and m2 concute a high spring of natural length l0 is compressed completely and tied by a string. This system while conving with a velocity v0 along +ve x-axis pass thorugh the origin at t=0, at this position the string sanps, Position of mass m1 at time t is given by the equation x1t=v0(A/1−cosωt). Calculate (i) position of the particle m2 as a funcation of time, (ii) l0 in terms of A.
07:07View SolutionThe position of a particle at time t is given by the equation x(t) = V_(0)/A (1-e^(At)) V_(0) = constant and A > 0 Dimensions of V_(0) and A respectively are
06:01View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If m_(1)=10kg, m_(2)=6kg and g =10m//s^(2) then what is the acceleration of masses?
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
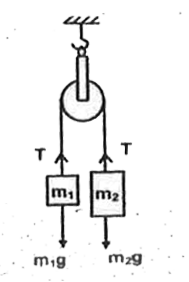
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?02:04View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?
01:26View Solutionप्रक्षेप्य गति में m1वm2 द्रव्यमानो के कणो के वेग समयt =0 पर क्रमशः →v1व →v2 है। ये समय t0पर टकराते है। उनके वेग समय 2t0 पर →v1 व→v2 हो जाते है जबकि अभी भी वे हवा में गतिमान है। तो
02:57View Solutionm1 व m2 द्रव्यमान के दो कण एक प्रक्षेप्य गति v1 में v2 वेग से गतिशील हैं। t=t0 समय पर टकराते हैं (प्रारम्भ से) तत्पश्चात् 2t0 समय पर उनकी वेग क्रमशः v'1 व v'2 पर हो जाते हैं, तब
[(m1v'1+m2v'2)−(m1v1−m2v2)]=?05:40View Solution

