Two particles are executing simple harmonic of the same amplitude (A) and frequency ω along the x-axis . Their mean position is separated by distance X_(0)(X_(0)gtA). If the maximum separation between them is (X_(0)+A), the phase difference between their motion is:Solution in Gujrati
π4
π6
π2
π3
The correct Answer is:D
X1=Asinωt
X2=X0+Asin(ωt+ϕ)
X2−X1=X0+Asin(ωt+ϕ)−Asinωt
Become |X2−X1|max=X0+A
|Asin(ωt+ϕ)−Asinωt|max=A
⇒ϕ=π3
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]
12 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MCQ s one or more than one correct answers
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [B]
104 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A particle of mass (m) is executing oscillations about the origin on the x axis. Its potential energy is V(x)=k|x|3 where k is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionThree simple harmonic motions in the same direction having the same amplitude and same period are superposed. If each differ in phase from the next by 45∘, then
View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.

View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionTwo particles are executing simple harmonic of the same amplitude (A) and frequency ω along the x-axis . Their mean position is separated by distance X0(X0>A). If the maximum separation between them is (X0+A), the phase difference between their motion is:
View Solutionx=x1+x2 (where x1=4cosωt and x2=3sinωt) is the equation of motion of a particle along x-axis. The phase different between x1 and x is
View SolutionFind the phase different between two particles executing simple harmonic motion with the same amplitude and frequency when their phases at a certain moment are as shown in the figure.
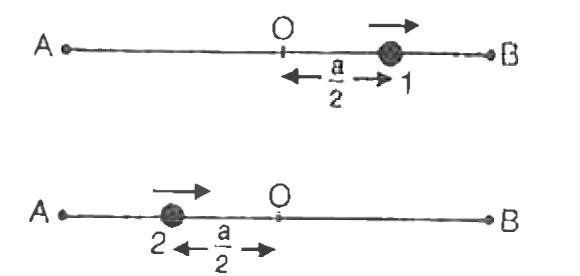
View SolutionTwo particles are executing simple harmonic of the same amplitude (A) and frequency ω along the x-axis . Their mean position is separated by distance X_(0)(X_(0)gtA). If the maximum separation between them is (X_(0)+A), the phase difference between their motion is:
View SolutionTwo particles are executing simple harmonic motion of the same amplitude A and frequency omega along the x-axis. Their mean position is separated by distance X_(0)(X_(0)gt A) . If the maximum separation between them is (X_(0)+A) , the phase difference between their motion is
View SolutionThe maximum seperation between two particles executing simple harmonic motion of the equal amplitude and same frequency along the same straight line and about the same mean position, is sqrt(3) times the amplitude of oscillation. IF the phase difference between them is phi , determine 2pi//phi .
View SolutionWrite equation of SHM of angular frequency ω and amplitude xm if the particle is situated at xm/√2 at t= 0 and is going toward mean position.
View SolutionTwo particles execute SHM about a common mean position with equal amplitudes along same line with amplitude of 12cm.If phase difference between the two particles is 2π3,the maximum separation between the particles is
View Solutionदो कण X-अक्ष के अनुदिस सामान आयाम A तथा आवर्ती ω से सरल आवर्त गति कर रहे है उनकी मध्य अवस्था के बीच दुरी x0,(x0>A) है यदि उनके बीच अधिकतम दूरी (x0+A) है तब उनकी गति में कालांतर है
View Solutionएक कण साम्यावस्था x=0 से x-अक्ष के अनुगत (x-अक्ष पर ) सरल आवर्त गति करता है। दोलन आवृति ω=4.00 प्रति सेकण्ड है। एक निश्चित सयम पर कण का निर्देशांक x0=25.0 सेमी है तथा इसका वेग v_(x_(0))=100सेमी//से^(2) है।
दोलन का आयाम बताओ
View SolutionA particle moves on the x-axis according to the equation x=x_(0) sin 2wt . The motion is simple harmonic.
View Solution
