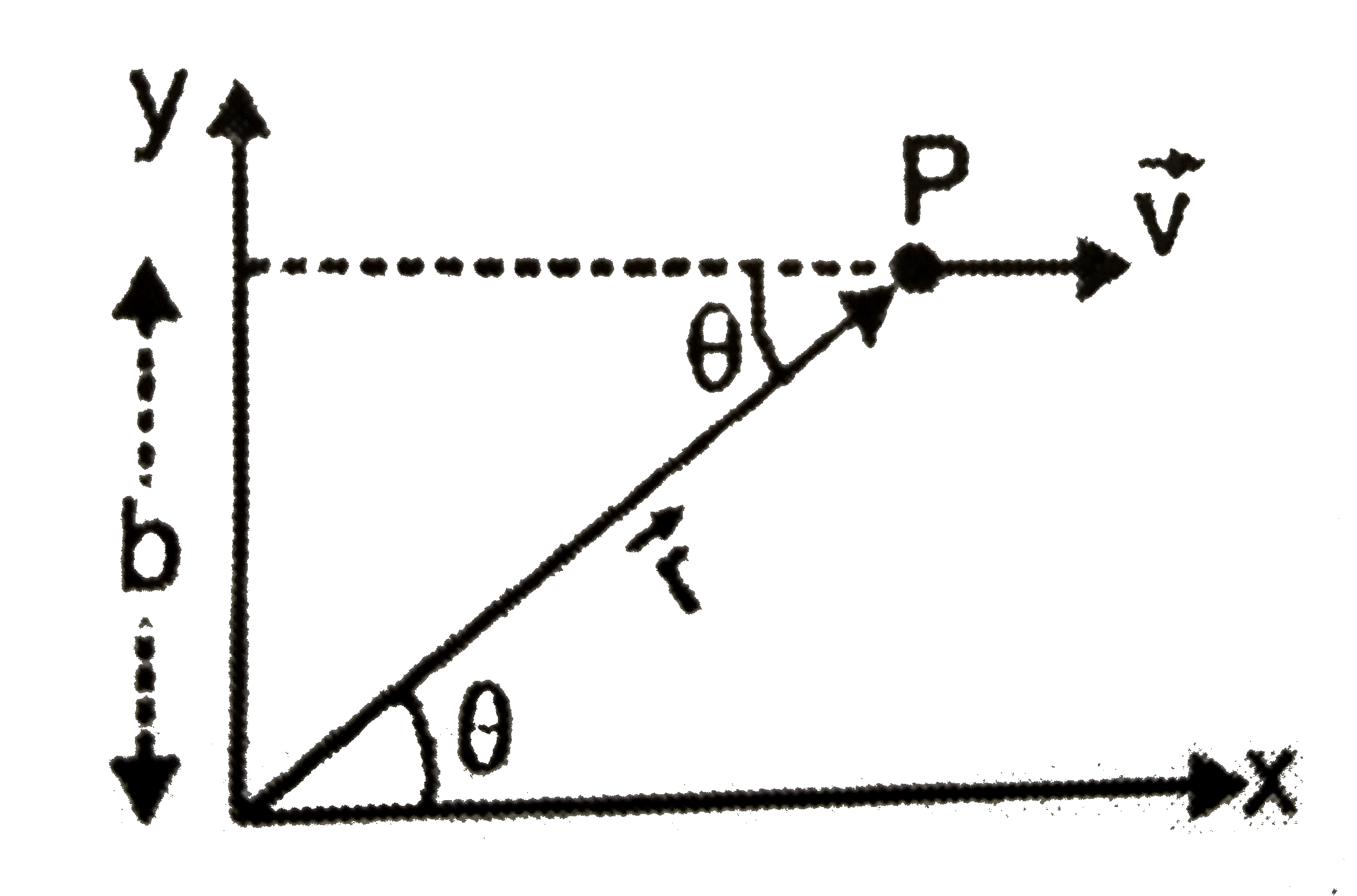
A particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle θ from the axis.
 Solution in Gujrati
Solution in Gujrati
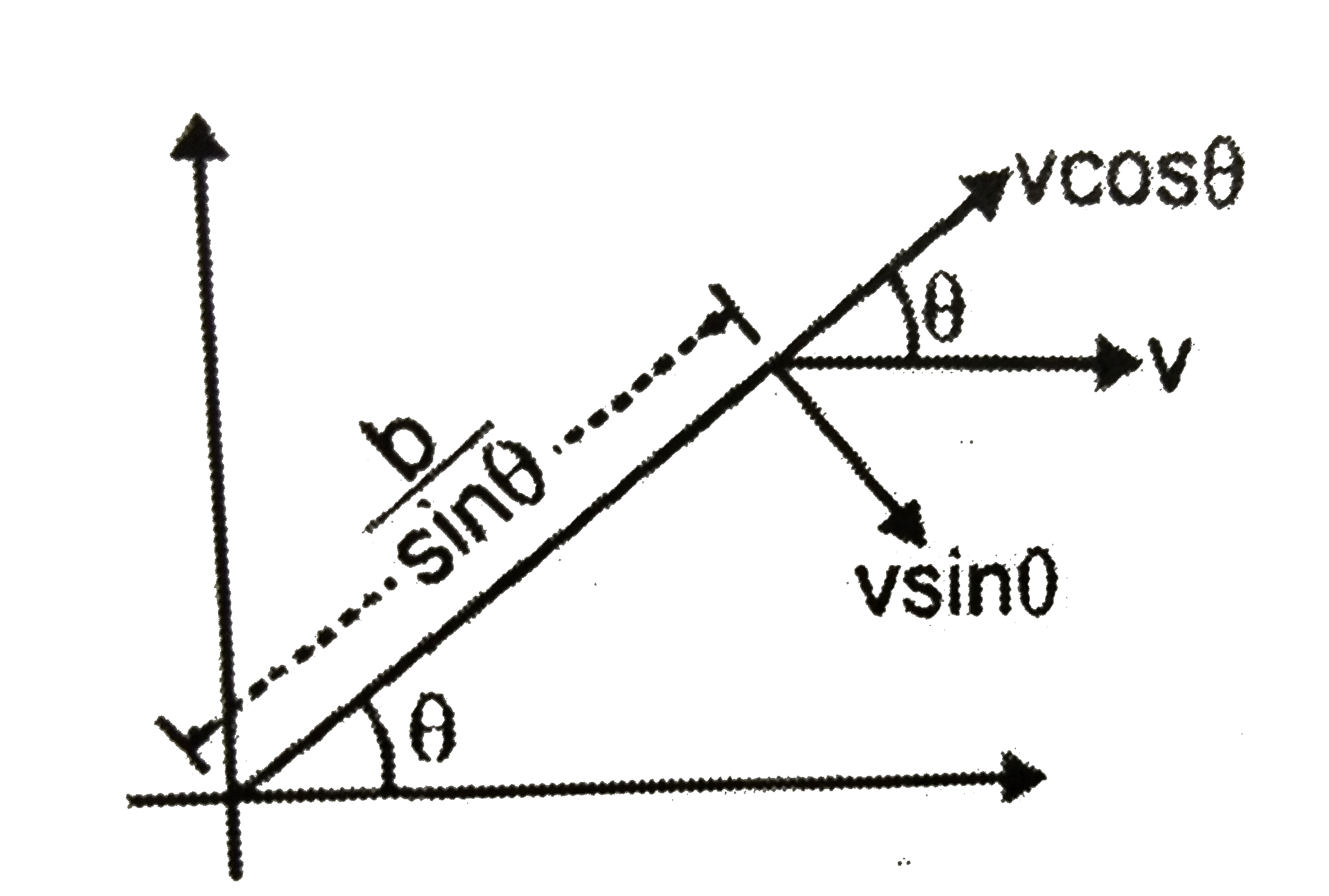
∴ωPO=vsinθbsinθ=vbsin2θ
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (S-1)
10 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - Dynamics of circular motion
8 Videos
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
A stone tied at the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 25 revolutions in 14 s, what is the magnitude of acceleration of the stone ?
View SolutionThe ball of mas m moves with speed v againest a smooth , fixed vertical circular groove of radius R kept on smooth horizontal surface find the
a. normal reaction of the floor or the ball.
b. normal reaction of the vertical wall on the ball.
View SolutionFind dydx for the following :
(i) y=x7/2 (ii) y=x−3
(iii)y=x (iv) y=x5+x3+4x1/2+7
(v) y=5x4+6x3/2+9x (vi) y=ax2+bx+C
(Vii)y=3x^(5)-3x-1/x
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View Solution
A particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O
View SolutionA particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle theta from the axis.
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle theta with x-axis.
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :

View SolutionA particle moves parallel to X-axis as shown in the figure such that at all instant the y axis component of its position vector is constant and is equal to 'b'. The angular velocity of the particle about the origin is
View SolutionA particle is going parallel to x - axis with constant speed V at a distance 'a' from the axis . Find its angular velocity about an axis passing the origin O , at the instant when radial vector of the particle makes angle theta with the x - axis
View SolutionA particle is moving with a contant velocity along a line parallel to positive X-axis. The magnitude of its angular momentum with respect of the origin is
View SolutionA particle is going parallel to x-axis with constant speed V at a distance 'a' from the axis. Find its angular velocity about an axis passing the origin O, at the instant when radial vector of the particle makes angle θ with the x-axis
View SolutionA particle is moving parallel to the x axis according to the image in such a way that the y of its position vector is fixed and is equal to b at every moment. Calculate the particle's angular relative to the point of origin when its radius along the vector x axis theta What angle to tell
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
View SolutionA particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle θ from the axis.

View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View Solution
