A particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
To solve the problem of finding the magnitude of the angular velocity of a particle moving along the line y=a at a constant speed v when its position makes an angle θ with the x-axis, we can follow these steps:
1. Understand the Position of the Particle:
The particle is moving along the line y=a. At a certain instant, it makes an angle θ with the x-axis. The coordinates of the particle can be expressed as (x,a).
2. Determine the Radius Vector:
The radius vector r is the distance from the origin to the particle. Since the particle is at position (x,a), we can express r using the right triangle formed:
r=√x2+a2
3. Relate the Radius to the Angle:
From the right triangle, we can express r in terms of a and θ:
rsinθ=a⟹r=asinθ
4. Calculate the Component of Velocity:
The particle moves with a constant speed v along the x-axis. To find the component of this velocity that is perpendicular to the radius vector, we note that the angle between the velocity vector (which is along the x-axis) and the radius vector can be determined. The perpendicular component of the velocity V⊥ is given by:
V⊥=vsinθ
5. Use the Relation Between Linear Velocity and Angular Velocity:
The relationship between linear velocity V, angular velocity ω, and radius r is given by:
V=rω
Rearranging this gives:
ω=V⊥r
6. Substitute the Values:
Now substituting V⊥ and r into the equation for ω:
ω=vsinθasinθ=vsin2θa
7. Final Result:
Thus, the magnitude of the angular velocity ω about the origin when the particle's position makes an angle θ with the x-axis is:
ω=vsin2θa
The particle is moving along the line y=a. At a certain instant, it makes an angle θ with the x-axis. The coordinates of the particle can be expressed as (x,a).
The radius vector r is the distance from the origin to the particle. Since the particle is at position (x,a), we can express r using the right triangle formed:
r=√x2+a2
From the right triangle, we can express r in terms of a and θ:
rsinθ=a⟹r=asinθ
The particle moves with a constant speed v along the x-axis. To find the component of this velocity that is perpendicular to the radius vector, we note that the angle between the velocity vector (which is along the x-axis) and the radius vector can be determined. The perpendicular component of the velocity V⊥ is given by:
V⊥=vsinθ
The relationship between linear velocity V, angular velocity ω, and radius r is given by:
V=rω
Rearranging this gives:
ω=V⊥r
Now substituting V⊥ and r into the equation for ω:
ω=vsinθasinθ=vsin2θa
Thus, the magnitude of the angular velocity ω about the origin when the particle's position makes an angle θ with the x-axis is:
ω=vsin2θa
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration4videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE21videos
TEST 1
Similar Questions
A particle of mass m is moving with constant speed v on the line y=b in positive x-direction. Find its angular momentum about origin, when position coordinates of the particle are (a, b).
View SolutionA particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is
 View Solution
View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionA particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
 View Solution
View SolutionA particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle θ from the axis.
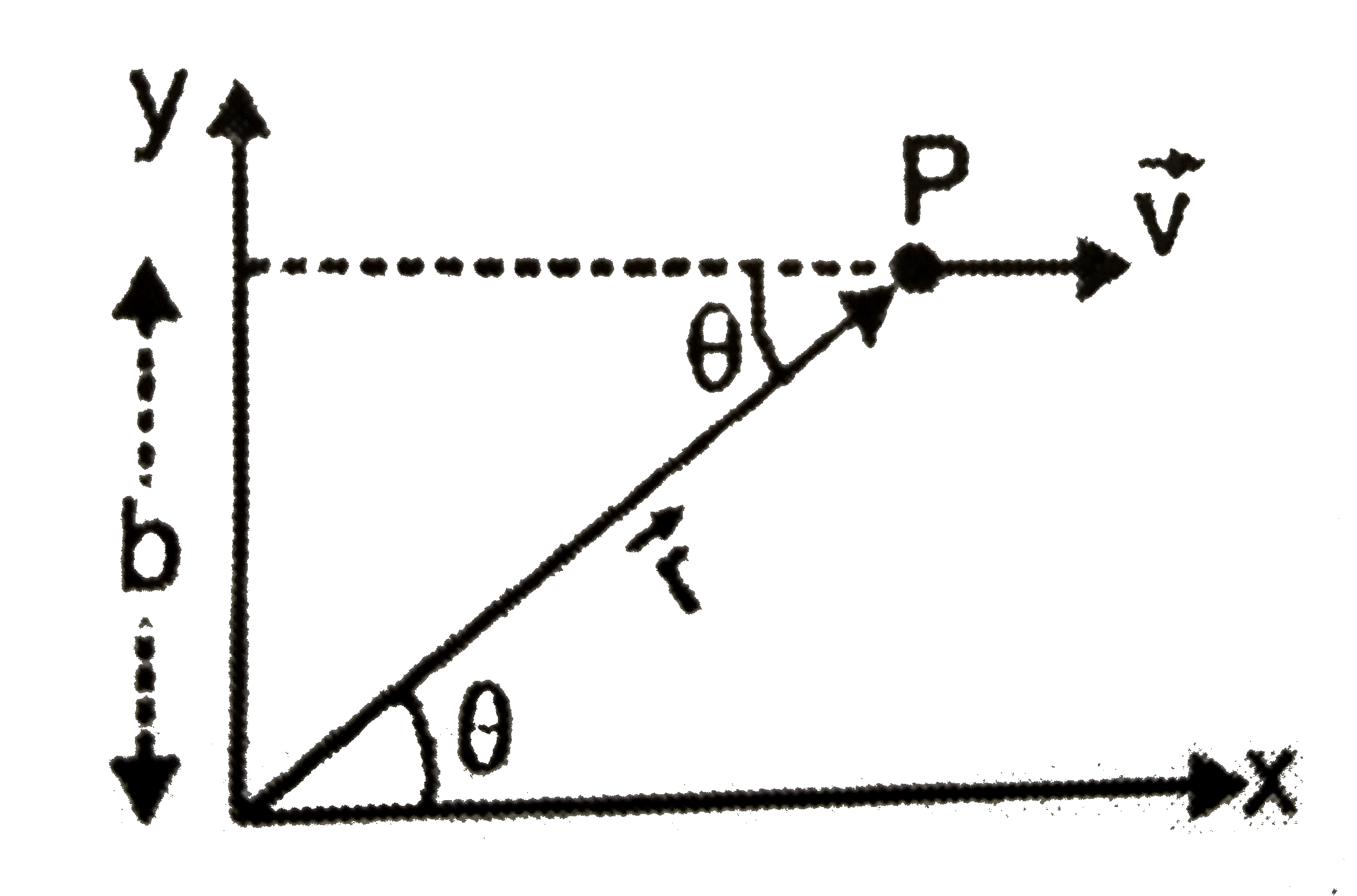 View Solution
View SolutionAcceleration of particle moving along the x-axis varies according to the law a=−2v, where a is in m/s2 and v is in m/s. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of time t.
(b) Find its position x as function of time t.
(c) Find its velocity v as function of its position coordinates.
(d) find the maximum distance it can go away from the origin.
(e) Will it reach the above-mentioned maximum distance?View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View SolutionA particle is moving on a circular path with constant speed v. The magnitude of the change in its velocity after it has described an angle of 90∘ is :
View SolutionA car is moving in a circular path with a uniform speed v. Find the magnitude of change in its velocity when the car rotates through an angle θ.
View Solution

