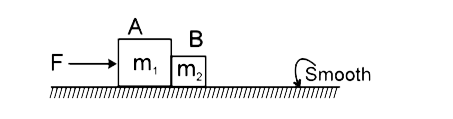
When force F applied on m2 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is no relative motion between m1andm2
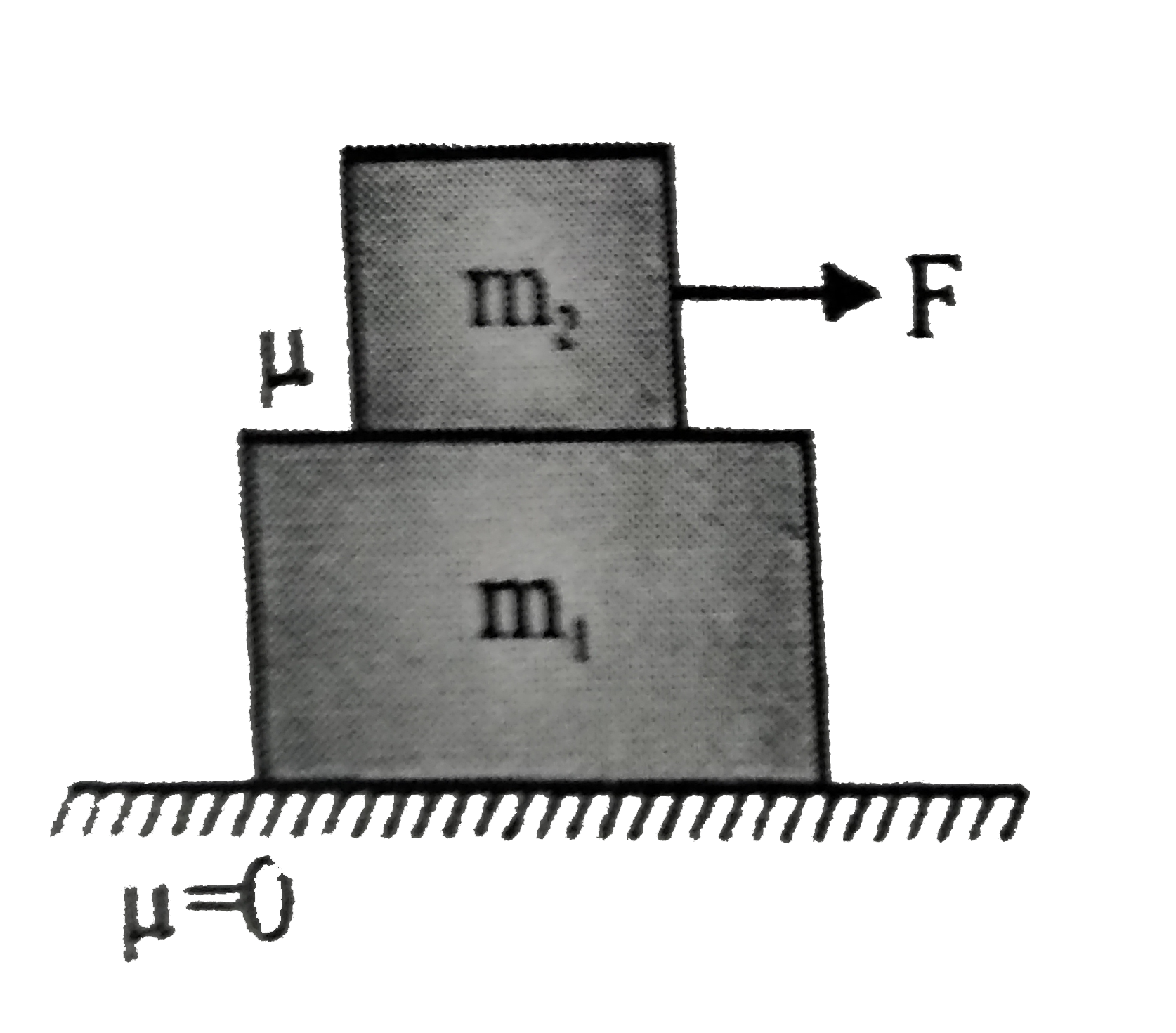 Solution in Gujrati
Solution in Gujrati
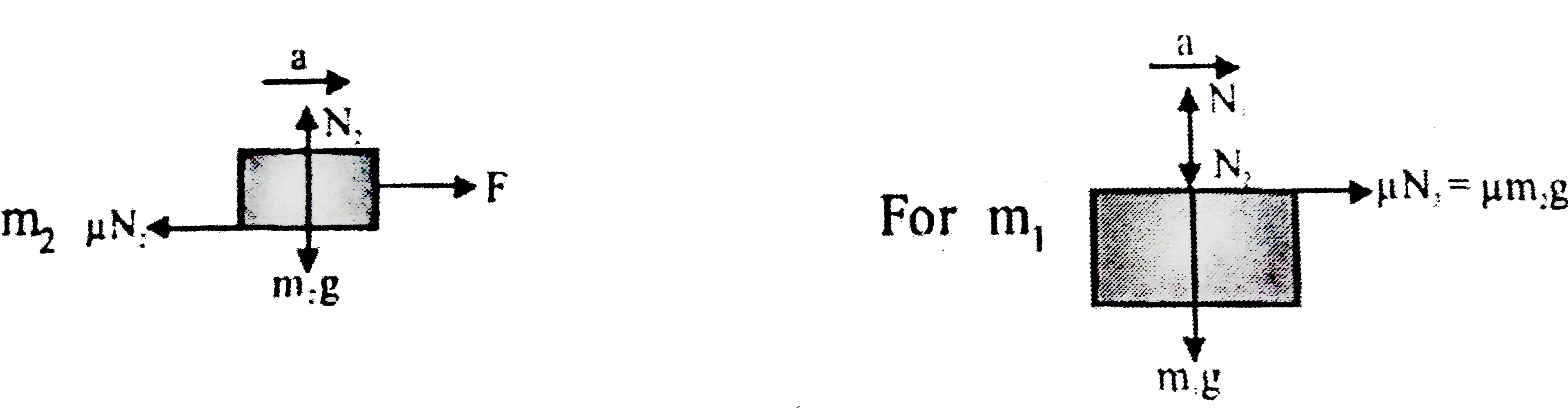
for system : acceleration =Fm1+m2
for m1:μm2g=m1a=m1(Fm1m2),Fmin=(m1+m2)(μ2gm1)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-1)
25 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-2)
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
A force F applied to an object of mass m1 produces an acceleration of 3.00m/s2. The same force applied to a second object of mass m2 produces an acceleration of 1.00m/s2.
(i) What is the value of the ratio m1/m2 ?
(ii) If m1andm2 are combined, find their acceleration under the action of the force F.
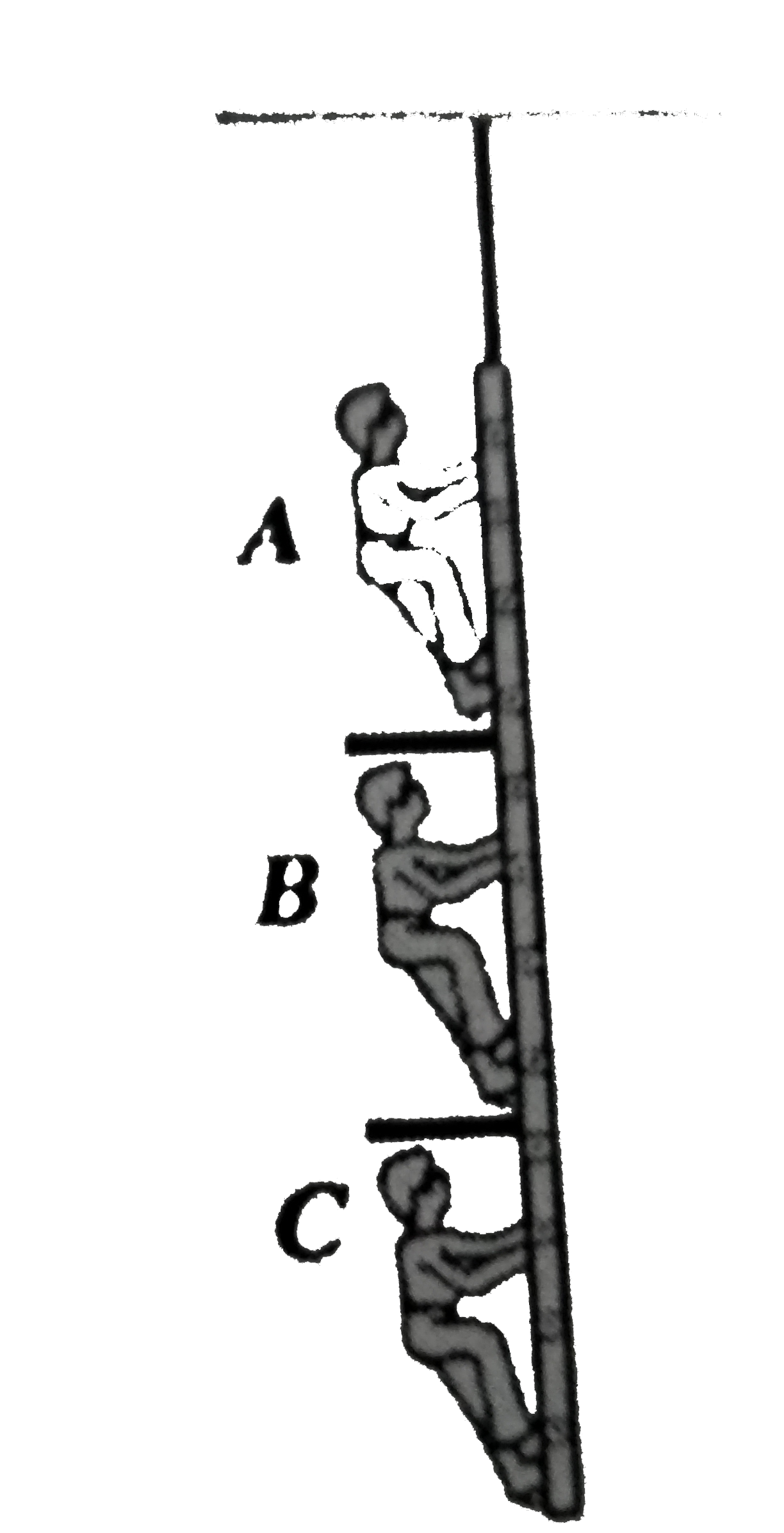
View SolutionA ladder is hanging from ceiling as shownin figure. Three men A, B and C of masses 40 kg, 60 kg, and 50 kg are climbing the ladder. Man A is going up with retardation 2m/s2, C is going up with an acceleration of 1m/s2 and man B is going up with a constantg speed of 0.5 m/s. Find the tension in the string supporting the ledder. [g=9.8m/s2]
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionThe block each of mass 1kg are placed as shown .They are connected by a string which passes over a smooth (massless) pulley.

There is no friction between m1 and the ground.The coefficient of friction between m1 andm2 is 0.2A force F is applied to m2. Which of the fpllowing statement is/are correct?
View SolutionIn the figure shown m_(1)=5 kg,m_(2) = 10 kg & friction coefficient between m_(1) & m_(2) is mu=0.1 and ground is frictionless then :
View SolutionWhat force F must be applied so that m_(1) and m_(2) are at rest on m_(3) in
View SolutionIn Fig.7.125, coefficient of friction between m_(1) and m_(2) is mu and that between m_(1) and the wall is zero. A force F is pressing the system against the wall. Minimum value of force required to hold the system in equilibrium is :
View SolutionIf, in Q.19, coefficient of friction between m1 and the wall is μ,and f1 and f2 are respectively, the force of friction on m1 and m2, then :
View SolutionTwo blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.



View SolutionWhen force F applied on m_(1) and surface. Is mu_(1) and the coefficient of friction between m_(1) and m_(2) is mu_(2). What should be the minimum value of F so that there is no relative motion between m_(1) and m_(2).
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
View SolutionTwo blocks m1=1kg, m2=2kg are placed one upon the other. m1 is kept on m2. The force of static friction between m1 and m2 is 0.2 and between m2 and the horizontal surface and the floor is 0.28. Calculate the maximum force that can be applied on m2 so that m1 and m2 does not get separated.(g=10ms−2)
View SolutionThe arrangement shown in the figure, the systme of masses m_(1), m_(2) and m_(3) is being pushed by a force F applied on m_(1) horizontally. In order to prevent the downwards slipping of m_(2) between m_(1) and m_(3) if coefficient of friction between m_(2) and m_(3) is mu and all the other surface are smooth, the minimum value of F :
View SolutionA force F is applied horizontally on mass m1 as shown in figure. Find the contact force between m1 and m2
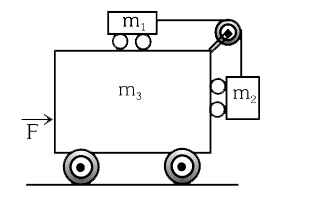
View SolutionAll surfaces assumed to be frictionless calculate the horizontal force F that must be applied so that m1 and m2 do not move relative to m3 is :–
View Solution
