If both roots are less than 3 then 'a' belongs to Solution in Gujrati
(32,3)
(−1,2)∪(2,3)
(−∞,2)
(2,∞)
The correct Answer is:C
Step by step video & image solution for If both roots are less than 3 then 'a' belongs to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - MATHEMATICS
34 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS SECTION-I
20 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - Chemistry
95 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLEN CHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
10 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
136 Videos
Similar Questions
5∑k=01sin[(K+1)θ]sin[(K+2)θ] can be equal to
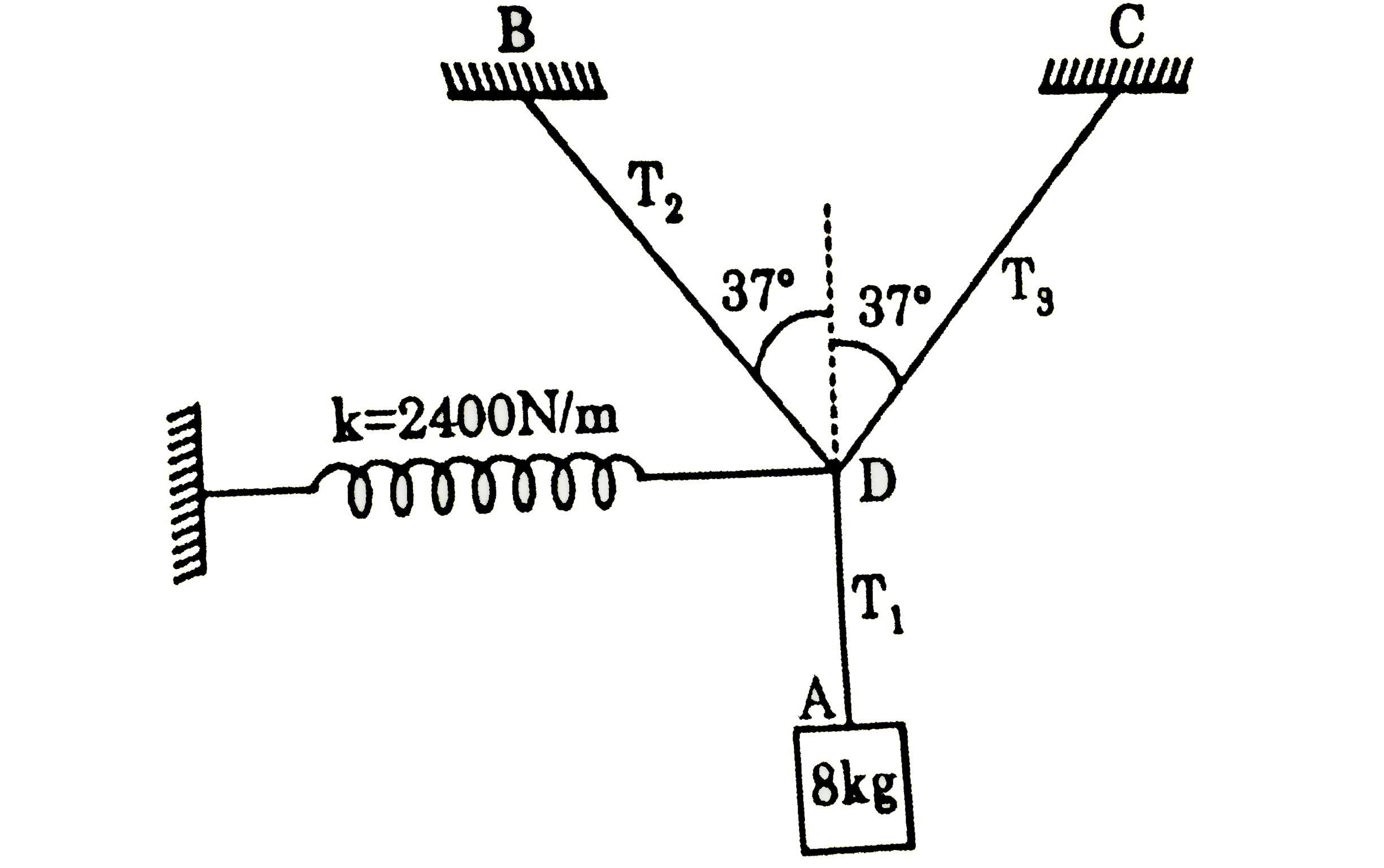
View SolutionGiven arrangement is in equilibrium and elongation in spring is 1cm. Tension in string AD is T1, in string BD is T2 and is string CD is T3.Choose correct values of T1,T2andT3:
View SolutionWhich of the following statement(s) is/are correct
View SolutionThe minimum value of the sum of real numbers a−5,a−4,3a−3,1,a8 and a10 with a>0 is
View SolutionIf a be sum of the odd numbered terms and b the sum of even numbered terms of the expansion (1+x)n,n ε N then (1−x2)n is equal to
View SolutionIf both the roots of ax2+ax+1=0 are less than 1, then find the exhaustive range of values of a.
View SolutionIf both the roots of the equation x^(2)-9x+a=0 are positive and one is greater than 3 and other is less than 3, then all possible values of a is-
View SolutionIf both roots of the quadratic equation x^(2)+x(4-2k)+k^(2)-3k-1=0 are less than 3, then k lies in the interval
View SolutionIf both roots are less than 3 then 'a' belongs to
View SolutionIf one root is greater then 3 and other root is less than 1 'a' belongs to
View SolutionDraw ogive (both ''less than'' and more than '' types) for the following distribution:
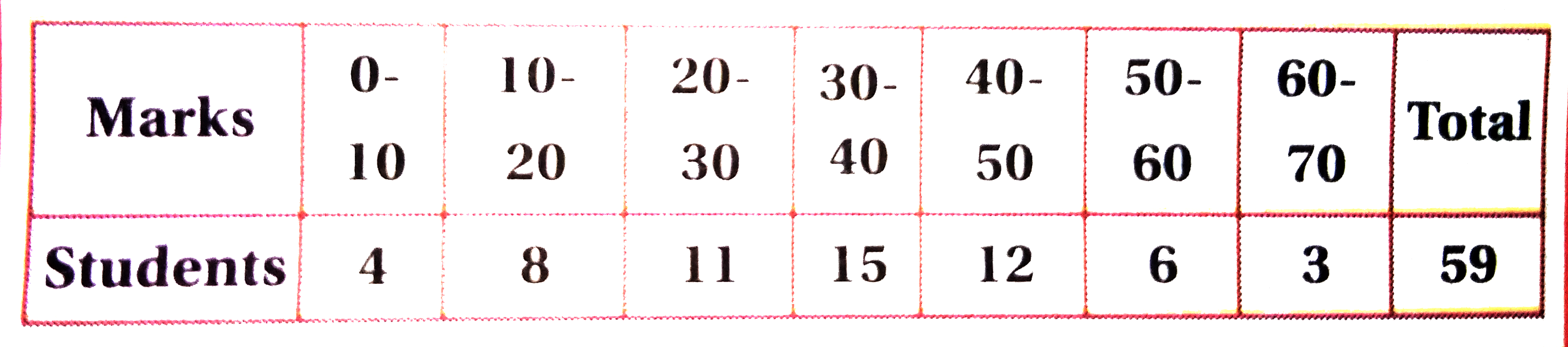
View SolutionMatch the following
Column-I Column -II(A) if the roots of the equationx2−2ax+a2+a−3=0 are real and less than 3, then a belongs to (p) a does not exist(B) If the roots of the equation x2−2ax+a2+a−3=0 are real and greater than , 3 then a belongs to (q) (32,3)(C) If exactly one root of the above equation lies in the interval (1,3) then a belongs to (r) (−1,2)∪(2,3)(D) IF the roots of the above equation are such that one root is greater than 3 and other smaller than 1, then a belongs to (s) (−∞,2)
View SolutionFind the set of all values of a for which the roots of the equation x2−2ax+a2+a−3=0 are less than 3,
View SolutionIf the both the roots of the quadratic equation x2−2kx+k2+k−5=0 are less than 5, then k
View SolutionBoth PH_(3) and NH_(3) are Lewis bases, but basic strength of PH_(3) is less than that of NH_(3) . Explain.
View SolutionIf both the roots of ax2+ax+1=0 are less than 1, then find the exhaustive range of values of a.
View Solution
