If one root is greater then 3 and other root is less than 1 'a' belongs to Solution in Gujrati
ϕ
(−1,2)∪(2,3)
(−∞,2)
(2,∞)
The correct Answer is:A
Step by step video & image solution for If one root is greater then 3 and other root is less than 1 'a' belongs to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - MATHEMATICS
34 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS SECTION-I
20 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - Chemistry
95 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLEN CHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
10 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
136 Videos
Similar Questions
5∑k=01sin[(K+1)θ]sin[(K+2)θ] can be equal to
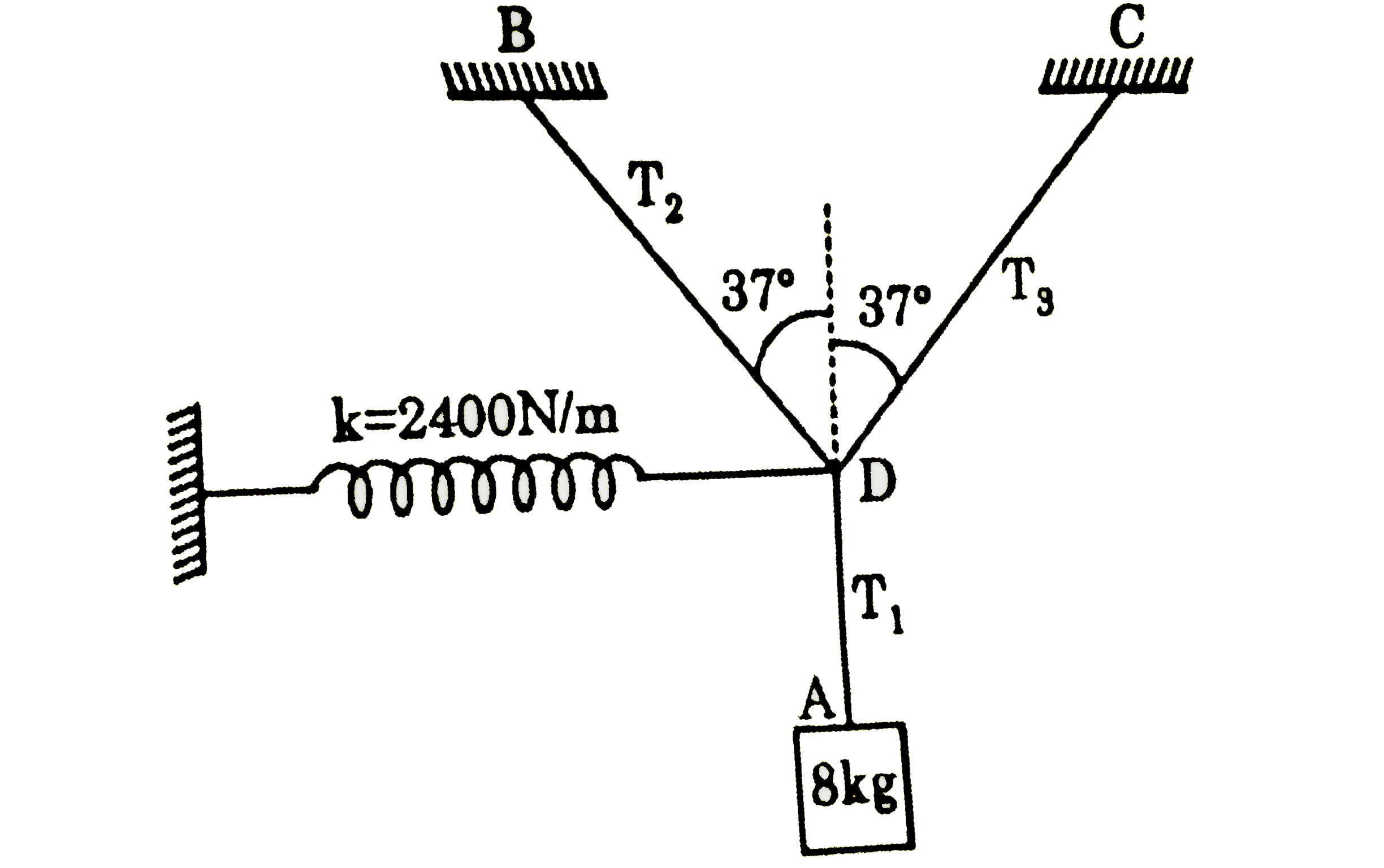
View SolutionGiven arrangement is in equilibrium and elongation in spring is 1cm. Tension in string AD is T1, in string BD is T2 and is string CD is T3.Choose correct values of T1,T2andT3:
View SolutionWhich of the following statement(s) is/are correct
View SolutionThe minimum value of the sum of real numbers a−5,a−4,3a−3,1,a8 and a10 with a>0 is
View SolutionIf a be sum of the odd numbered terms and b the sum of even numbered terms of the expansion (1+x)n,n ε N then (1−x2)n is equal to
View SolutionIf alpha,beta are the roots of the equation x^(2)-2p(x-4)-15=0 then the set of values of p for which one root is less than 1 and the other root is greater than 2 is
View SolutionThe value of lambda for which the equation 2x^(2)-2(2 lambda+1)x+lambda(lambda+1)=0 may have one root less than lambda and other root greater than lambda are given by
View SolutionIf one root of f(x)=0 is less than 1 and the other is greater than 2, where f(x)=x^(2)-ax+4, then a cannot be
View SolutionIf both the roots of the equation x^(2)-9x+a=0 are positive and one is greater than 3 and other is less than 3, then all possible values of a is-
View SolutionIf b>a then show that the equation (x−a)(x−b)−1=0 has one root less than a and other root greater than b.
View SolutionIf both roots are less than 3 then 'a' belongs to
View SolutionIf one root is greater then 3 and other root is less than 1 'a' belongs to
View Solutionfor what values of m, the equation 2x2−2(2m+1)x+m(m+1)=0m∈R has (i) Both roots smallar than 2 ? (ii) Both roots greater than 2 ? (iii) Both roots lie in the interval (2,3) ? (iv) Exactly one root lie in the interval (2,3) ? (v) One root is smaller than 1, and the other root is greater than 1 ? (vi) One root is greater than 3 and the other root is smaller than 2 ? (vii) Roots αandβ are such that both 2 and 3 lie between αandβ ?
View SolutionMatch the following
Column-I Column -II(A) if the roots of the equationx2−2ax+a2+a−3=0 are real and less than 3, then a belongs to (p) a does not exist(B) If the roots of the equation x2−2ax+a2+a−3=0 are real and greater than , 3 then a belongs to (q) (32,3)(C) If exactly one root of the above equation lies in the interval (1,3) then a belongs to (r) (−1,2)∪(2,3)(D) IF the roots of the above equation are such that one root is greater than 3 and other smaller than 1, then a belongs to (s) (−∞,2)
View SolutionOut of the two roots of x2+(1−2λ)x+(λ2−λ−2)=0 one root is greater than 3 and the other root is less than 3 ,then the limits of λ are
View SolutionThe values of a for which one root of the equation, x2+(2a+1)x+(a−2)=0 is greater than 1 and the other root less than zero, is
View Solution
