A projectile is projected from ground with initial velocity →u=u0ˆi+v0ˆj. If acceleration due to gragvity (g) is along the negative y-direction then find maximum displacement in x-direction. Solution in Gujrati
u202g
2u0v0g
v202g
4u0v0g
The correct Answer is:B
Horizontal range R=2uxuyg=2u0v0g
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2
170 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-3
41 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - PHY
75 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
The velocity of a particle moving with constant acceleration at an instant t0 is 10m/s After 5 seconds of that instant the velocity of the particle is 20m/s. The velocity at 3 second before t0 is:-
View SolutionAssertion : A body can have acceleration even if its velocity is zero at a given instant of time.
Reason : A body is momentarily at rest when it reverses its direction of motion.
View SolutionA particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?
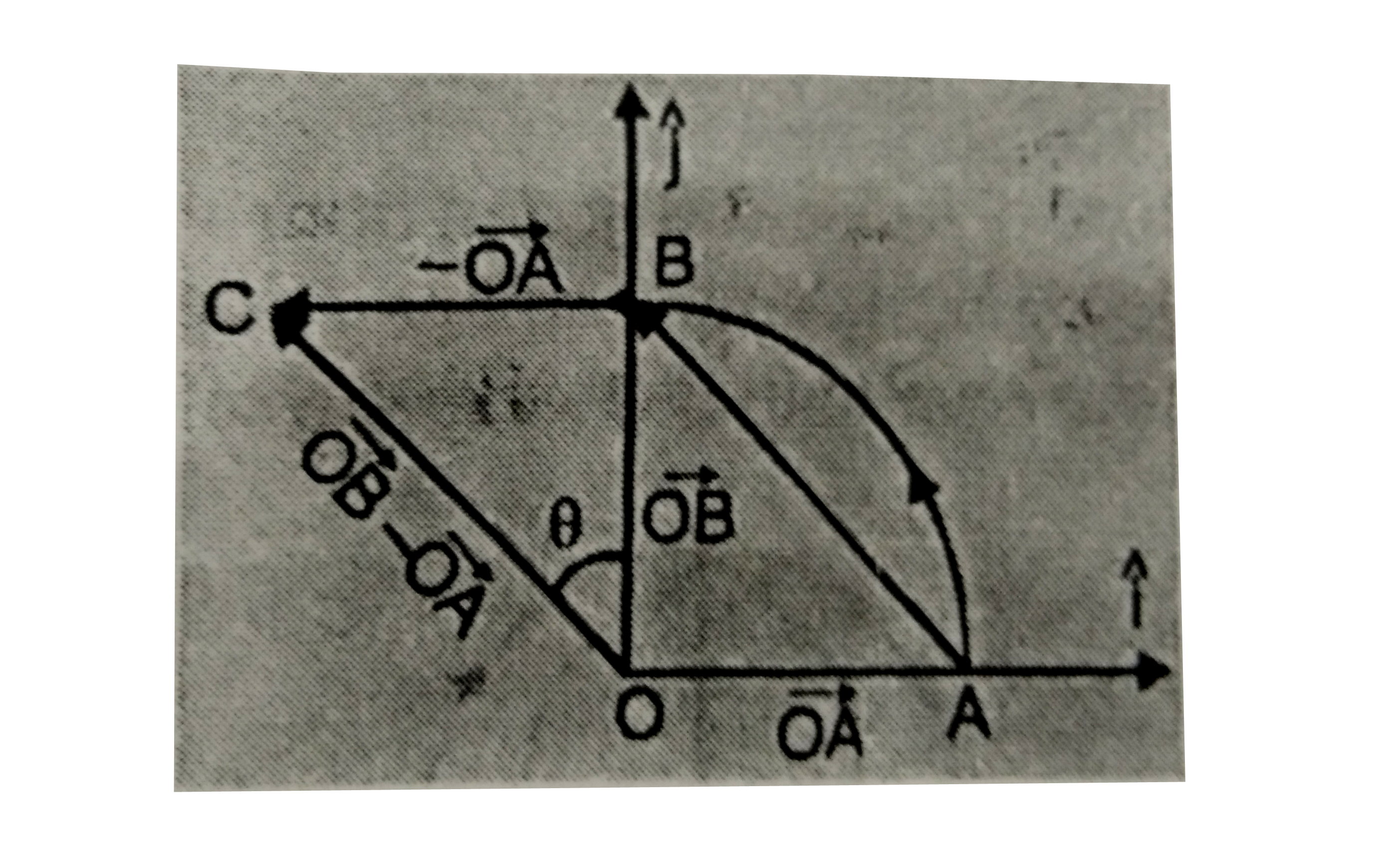
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionIf →u=aˆi+bˆj+cˆk with ˆi,ˆj,ˆkare in east, north and vertical directions, horizontal component of velocity of projectile is
View SolutionTwo projectiles are projected from same point on the ground in x-y plane with y direction as vertical. The initial velocity of projectiles are
→V1=Vx1ˆi+Yy1ˆj
→V2=Vx2ˆi+Vy2ˆj
It is given that Vx1>Vx2 and Yx1<Yx2. Check whether all of the following statment/s are True.
View SolutionA region has a uniform magnetic field B along positive x direction and a uniform electric field E in negative x direction. A positively charged particle is projected from origin with a velocity underset(V)to=V_(0)hati+V_(0)hatj . After some time the velocity of the particle was observed to be V_(0)hatJ while its x co-ordinate was positive. Write all possible values of (E)/(B)
View SolutionTwo unit vectors ˆi and ˆj are directed along x-axis and y-axis respectively. What is the magnitude and direction of the vectors ˆi+ˆjandˆi−ˆj?
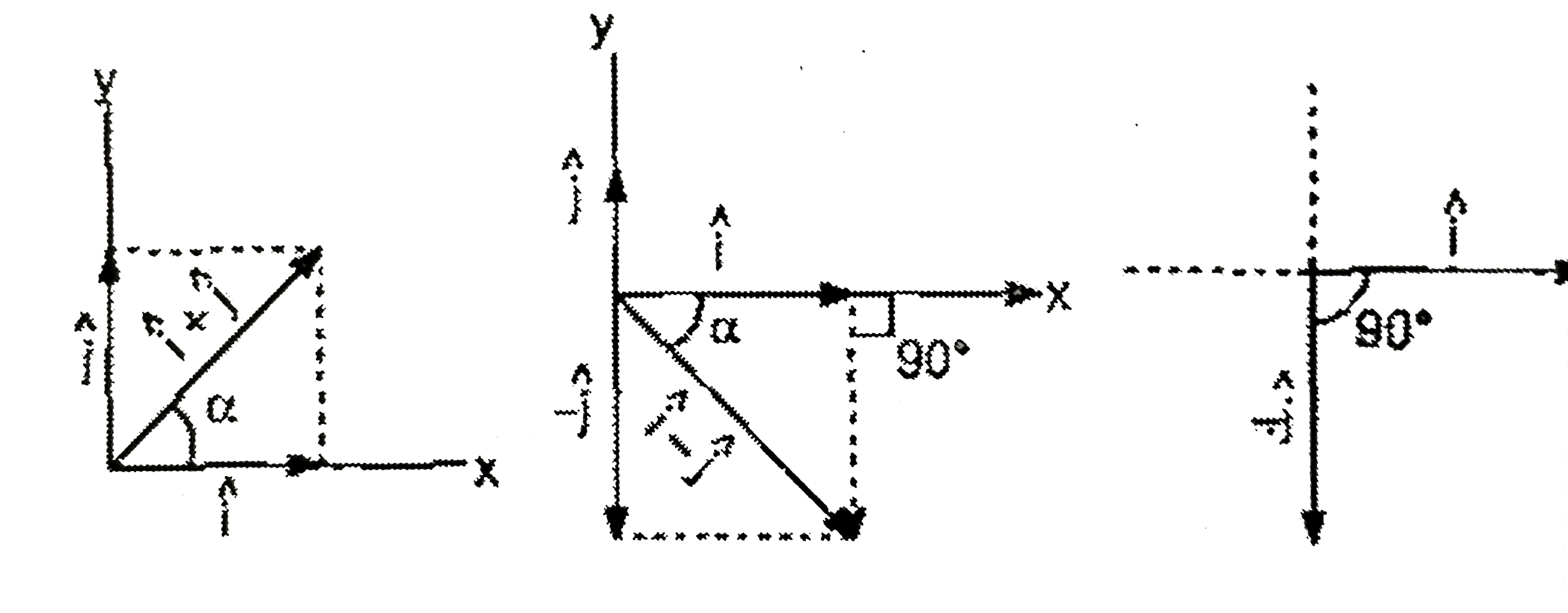
View SolutionIf hati and hatj are unit vectors along X-and Y-axis respective, then what is the magnitude and direction of hati +hatj and hati - hatj ?
View SolutionA projectile is projected from ground with initial velocity vecu=u_(0)hati+v_(0)hatj . If acceleration due to gragvity (g) is along the negative y-direction then find maximum displacement in x-direction.
View SolutionA projectile is thrown with an initial velocity (v_(x)hati + v_(y)hatj) ms^(-1) . If the range of the projectile is double the maximum height , then v_(y)/v_(x) is
View Solutionm द्रव्यमान का एक छोटा कण Xअक्ष से θ कोण पर प्रारम्भिक वेग v0 से x-y तल में चित्रानुसार प्रक्षेपित किया गया है। समय t<v0sinθg पर कण का कोणीय संवेग है:
जहां ˆi,ˆj,ˆk,x−,y− तथा z- अक्ष के अनुदिश एकांक सदिश है।
View Solutionˆi व् ˆj क्रमशः x- व् y- अक्षों के अनुदिश एकांक सदिश है सदिशों ˆi+ˆj तथा ˆi−ˆj का परिमाण तथा दिशा क्या होगा ? सदिश A=2ˆi+3ˆj के ˆi+ˆjव् ˆi−ˆj के दिशाओ के अनुदिश घातक निकालिये आप ग्राफ़िय विधि का उपयोग क्र सकता है
View SolutionThe initial velocity of a projectile is (hati+2hatj)m//s , where hati and hatj are unit vectors along the horizontal and vertical directions respectively. Find out the locus of the projectile , taking g=10 m//s^2 .
View SolutionA projectile is given an initial velocity of (ˆi+2ˆj)m/s, where ˆj is along the ground and ˆj is along the velocity. If g=10m/s2, the equation of its trajeclory is
View Solution
