Two resistance R1 and R2 are made of different material. The temperature coefficient of the material of R1 is α and of the material of R2 is −β. Then resistance of the series combination of R1 and R2 will not change with temperature, if R1/R2 will not change with temperature if R1/R2 equalsSolution in Gujrati
αβ
α+βα−β
α2+β2αβ
βα
The correct Answer is:4
Step by step video & image solution for Two resistance R_(1) and R_(2) are made of different material. The temperature coefficient of the material of R_(1) is alpha and of the material of R_(2) is -beta. Then resistance of the series combination of R_(1) and R_(2) will not change with temperature, if R_(1)//R_(2) will not change with temperature if R_(1)//R_(2) equals by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In which of the following the carriers of electric current are electrons only? A) SUPER CONDUCTOR B) A VOLTAIC CELL C) A SEMICONDUCTOR D) A HYDROGEN DISCHARGE TUBE
View SolutionA ball of mass (m)0.5kg is attached to the end of a string having length (L)0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of angular velocity of ball (radian/s) is -
 .
.
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View Solution(r_(3)+r_(1))(r_(3)+r_(2))sin C=2r_(3)sqrt(r_(2)r_(3)+r_(3)r_(1)+r_(1)r_(2))
View SolutionTwo resistors of resistances R_(1)=100 pm 3 ohm and R_(2)=200 pm 4 ohm are connected (a) in series, (b) in parallel. Find the equivalent resistance of the (a) series combination, (b) parallel combination. Use for (a) the relation R=R_(1)+R_(2) and for (b) 1/(R')=1/R_(1)+1/R_(2) and (Delta R')/R'^(2)=(Delta R_(1))/R_(1)^(2)+(Delta R_(2))/R_(2)^(2)
View SolutionSpace between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
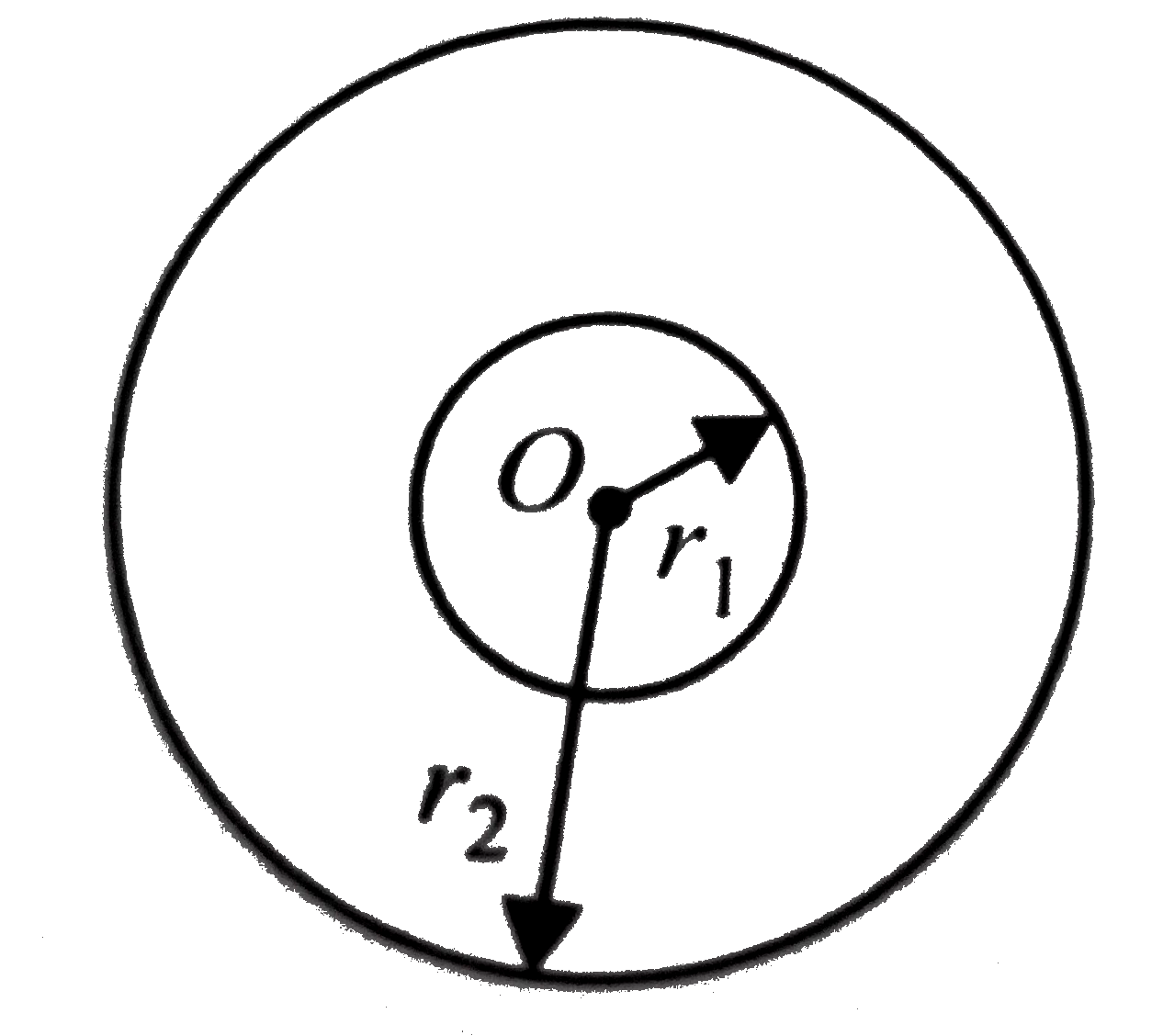
View SolutionR1,R2R2,,,… प्रतिरोध के अनेक प्रतिरोधक श्रेणीक्रम में संयोजित है तथा संयोजन के सिरों के बीच स्थायी विभवांतर V आरोपित किया गया है। परिपथ का तुल्य प्रतिरोध Rs है तथा R1,R2,R3,.... के सिरों के बीच विभवांतर क्रमशः V1,V2,V3,... है ।
View Solutionदो प्रतिरोध R1 और R2 भिन्न पदार्थो के बने हुए है । R1के पदार्थ का प्रतिरोध ताप गुणांक α और R2 के पदार्थ का प्रतिरोध ताप गुणांक −β है । R1और R2 के श्रेणीक्रम संयोजन का प्रतिरोध ताप के साथ परिवर्तित नहीं होगा यदि R1R2का मान होगा -
View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
View Solution5 resistances R_(1), R_(2),R_(3),R_(4),R_(5) are joined as shown in the figure. The values of R_(1), R_(2), R_(3) and R_(4) are so adjusted that the current in the circuit does not change for any value of the resistance R_(5) . This is possible for the following relation
View SolutionStatement-1: ln !ABC,r1+r2+r3−r=4R
Statement-2: In !ABC,r1r2+r2r3+r3r1=!2
View SolutionA resistance R_(2) is connected in parallel with a resistance R_(1) what resistance R_(3) must be connected in series with the combination of R_(1) and R_(2) so that the equivalent resistance is equal to the resistance R_(1) -
View Solution[" Two cells of equal e.m.f.and of internal "],[" resistances "r_(1)" and "r_(2)(r_(1)>r_(2))" are "],[" connected in series.On connecting this "],[" combination to an external resistance "R" ,"],[" it is observed that the potential "],[" difference across the first cell becomes "],[" zero.The value of "R" will be "],[[" (A) "r_(2)(r_(1)>r_(2)),(r_(1)+r_(2))/(2)],[" (B) "r_(1)-r_(2),(r_(1)-r_(2))/(2)]]
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionIn a ΔABC, if 2r2r3r2−r1=r3−r1 then
r1(r2+r3)√r1r2+r2r3+r3r1=
View SolutionThe possible percentage error in computing the parallel resistance R of three resistances R1,R2,R3 from the formula 1R=1R1+1R2+1R3, if R1,R2,R3 are each 1.2% in error, is
View Solution
