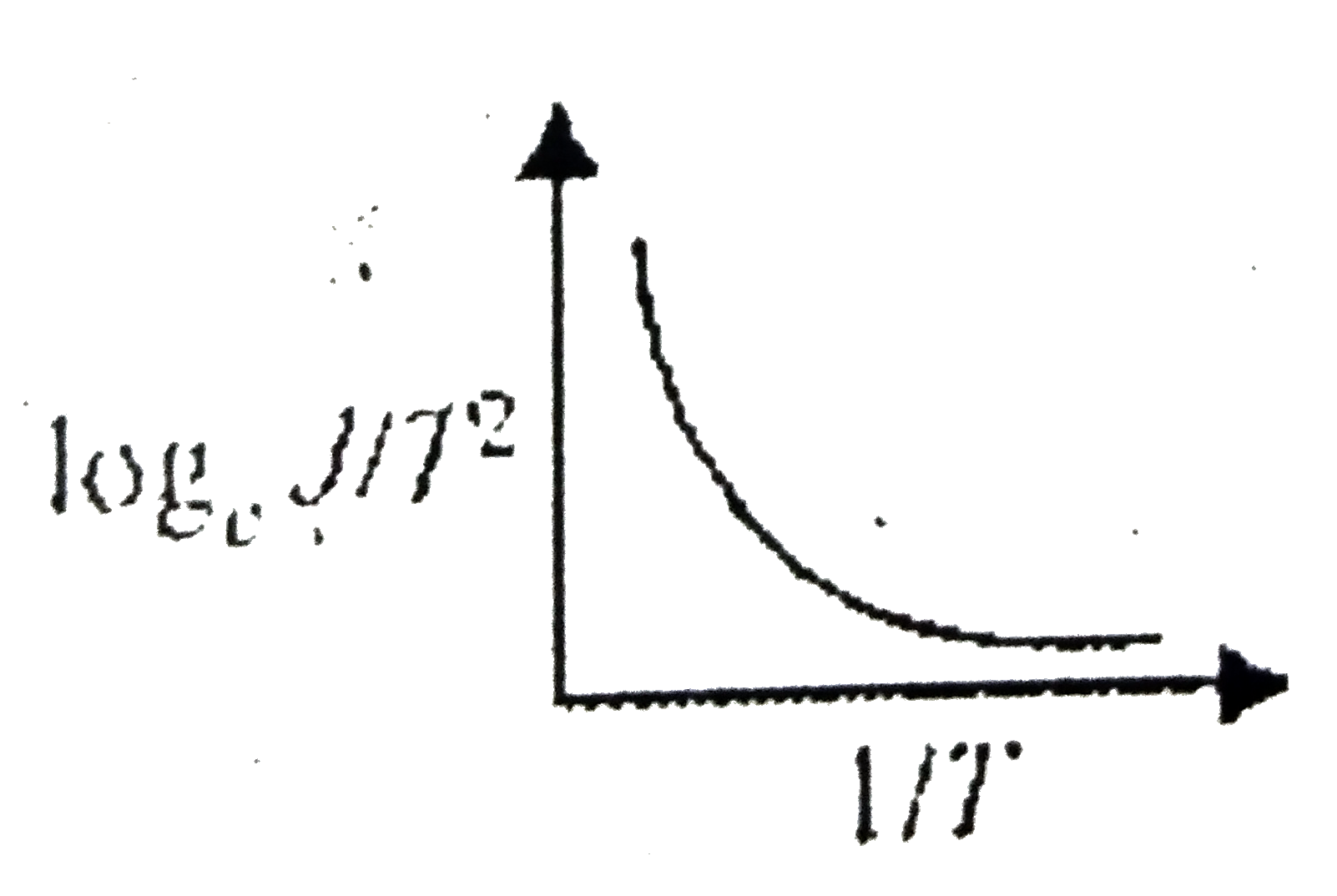
The current curve between logejT2 and lT


The correct Answer is:A
To solve the question regarding the current curve between loge(jT2) and 1T, we can follow these steps:
1. Understand the Relationship:
We start with the relationship given in the problem:
j=aT2e−bT
where a and b are constants.
2. Rearranging the Equation:
We can express jT2:
jT2=ae−bT
3. Taking the Natural Logarithm:
Now, we take the natural logarithm (base e) of both sides:
loge(jT2)=loge(a)+loge(e−bT)
4. Simplifying the Logarithm:
Using the property of logarithms loge(ex)=x, we can simplify the right side:
loge(jT2)=loge(a)−bT
5. Rearranging the Equation:
We can rearrange this equation to express it in the form of a straight line:
loge(jT2)=−bT+loge(a)
6. Identifying the Variables:
In this equation, we can identify:
- y=loge(jT2)
- x=1T
- The slope m=−b
- The y-intercept c=loge(a)
7. Conclusion:
The relationship between loge(jT2) and 1T is linear, with a negative slope. Thus, the correct option that represents this relationship is:
loge(jT2) vs 1T
We start with the relationship given in the problem:
j=aT2e−bT
where a and b are constants.
We can express jT2:
jT2=ae−bT
Now, we take the natural logarithm (base e) of both sides:
loge(jT2)=loge(a)+loge(e−bT)
Using the property of logarithms loge(ex)=x, we can simplify the right side:
loge(jT2)=loge(a)−bT
We can rearrange this equation to express it in the form of a straight line:
loge(jT2)=−bT+loge(a)
In this equation, we can identify:
- y=loge(jT2)
- x=1T
- The slope m=−b
- The y-intercept c=loge(a)
The relationship between loge(jT2) and 1T is linear, with a negative slope. Thus, the correct option that represents this relationship is:
loge(jT2) vs 1T
Similar Questions
A liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
View SolutionThe graph between log t1/2 and log a at a given temperature is
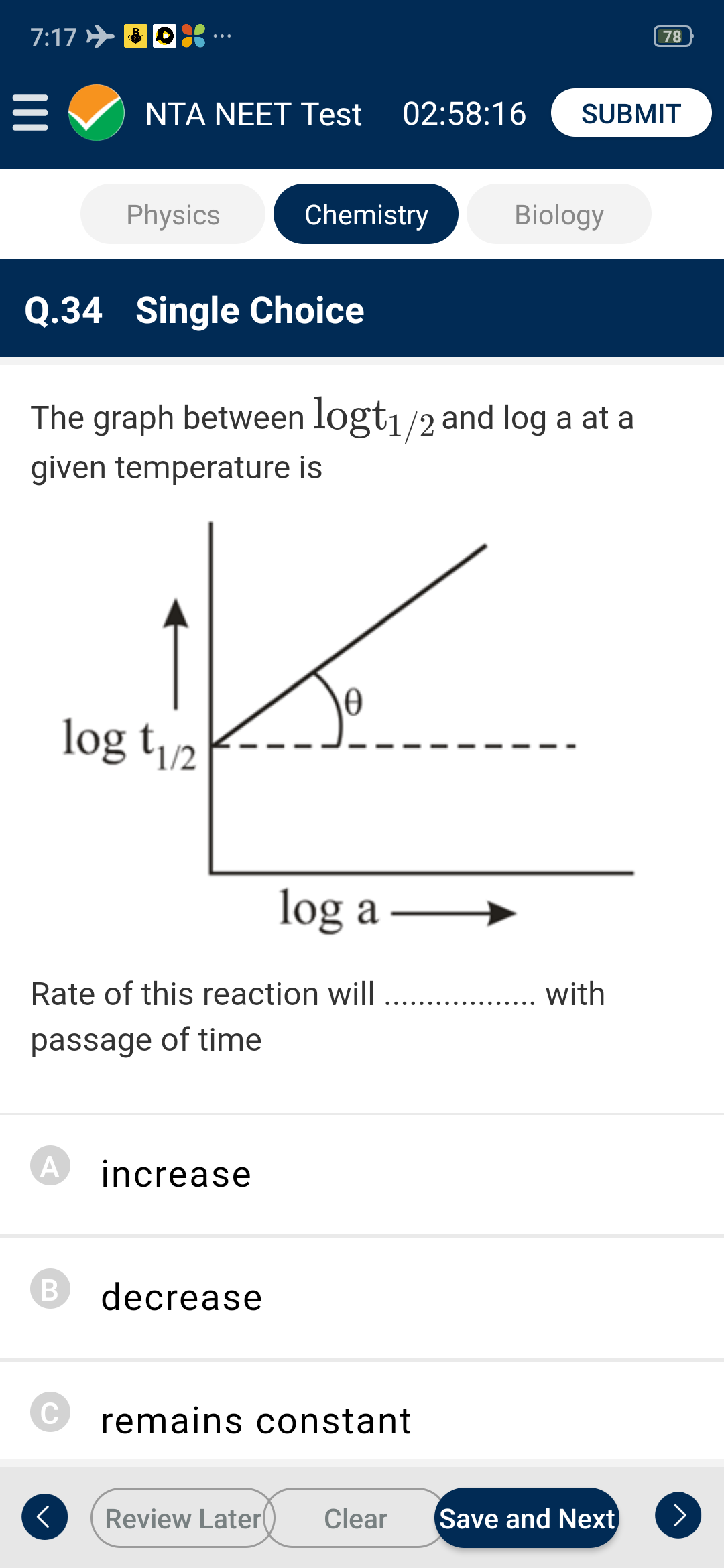
Rate of this reaction will …….with passage of time
View SolutionThe area enclosed between the curve y=loge(x+e) and the coordinate axes is
View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is (a) 2sq.units (b) 1sq.units (c) 4sq.units (d) none of these
View SolutionFind the area enclosed between the curves: y=loge(x+e),x=loge(1y) & the x-axis.
View SolutionConsider the circuit shown below. When switch S1 is closed, let I be the current at time t, then applying Kirchhoff's law
E−iR−Ldidt=0or∫i0diE−iR=1L∫10dt
i=ER(1−e−Rl⋅t)
LR = time constant of circuit
When current reaches its steady value (=i0, open S1 and close S2, the current does reach to zero finally but decays expnentially. The decay equation is given as i=i0e−RL⋅T).
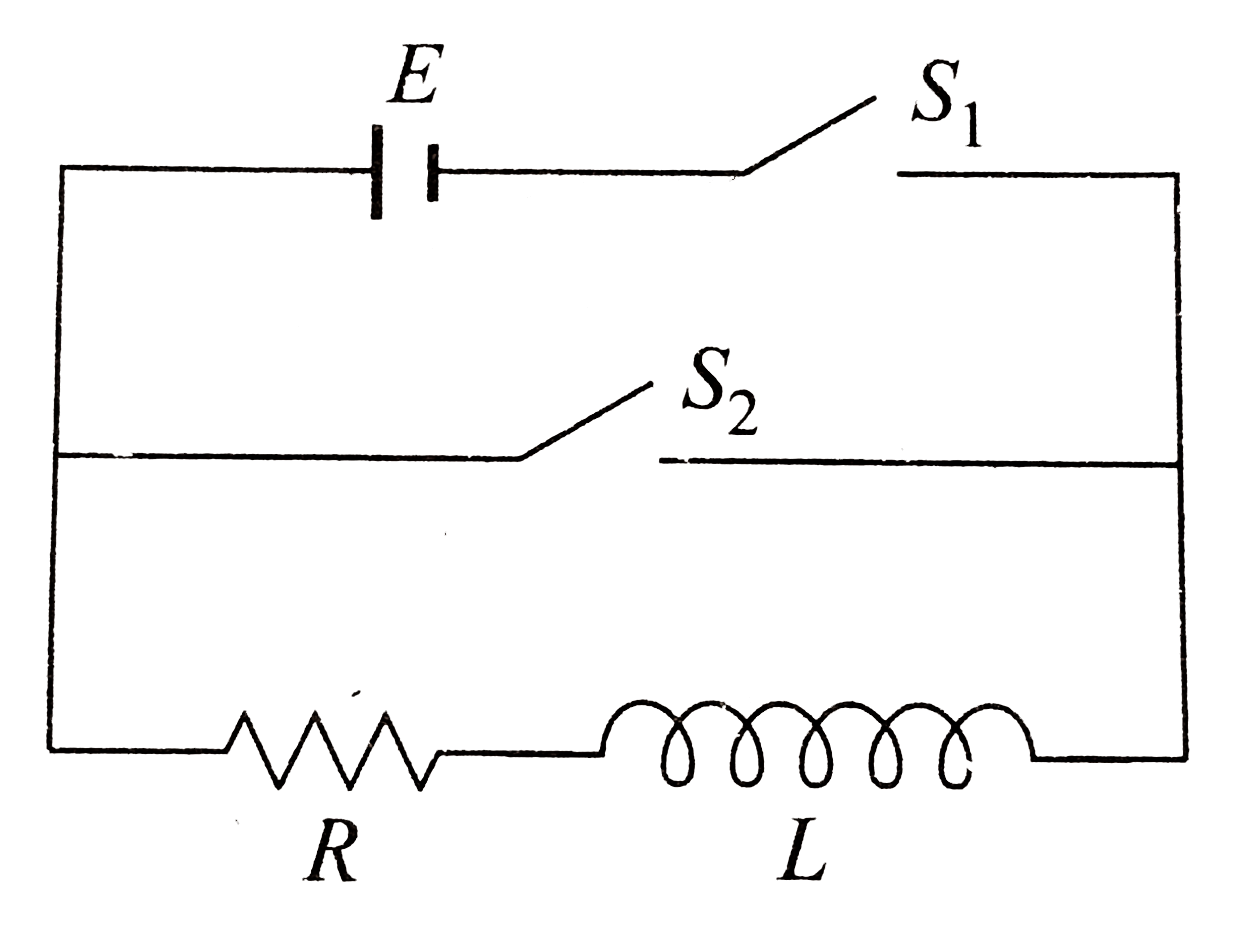
When a coil carrying a steady current is short circuited, the current decreases in it η times in time t0. The time constant of the circuit is
View SolutionWhat type of graph do you expect between (i) L and T and (ii) L and T^2 ?
View SolutionAn L-R circuit has a cell of e.m.f. E , which is switched on at time t = 0. The current in the circuit after a long time will be
View SolutionA curve is represented parametrically by the equations x=etcostandy=etsint where t is a parameter. Then The relation between the parameter 't' and the angle a between the tangent to the given curve andthe x-axis is given by, 't' equals
View SolutionThe minimum distance between a point on the curve y=ex and a point on the curve y=logex is
View Solution
