Three identical charges are placed at corners of a equilateral triangel of side l. If force between any two charges is F, the work required to double the dimensiions of triangle is
−3Fl
3Fl
(−3/2)Fl
(3/2)Fl
The correct Answer is:C
To find the work required to double the dimensions of an equilateral triangle formed by three identical charges, we can follow these steps:
Step 1: Understand the Initial Configuration
We have three identical charges Q placed at the corners of an equilateral triangle with side length L. The force between any two charges is given as F.
Step 2: Calculate the Initial Potential Energy
The potential energy U between two point charges is given by the formula:
U=kQ1Q2r
For three identical charges at the corners of the triangle, the potential energy due to each pair of charges is:
Upair=kQ2L
Since there are three pairs of charges (between each pair of corners), the total initial potential energy Ui is:
Ui=3⋅kQ2L=3kQ2L
Step 3: Calculate the Final Potential Energy
When the dimensions of the triangle are doubled, the new side length becomes 2L. The potential energy for each pair of charges in the new configuration is:
U′pair=kQ22L
The total final potential energy Uf is:
Uf=3⋅kQ22L=3kQ22L
Step 4: Calculate the Work Done
The work done W by an external agent to change the configuration is equal to the change in potential energy:
W=Uf−Ui
Substituting the values we calculated:
W=3kQ22L−3kQ2L
To simplify, we can factor out 3kQ2L:
W=3kQ2L(12−1)=3kQ2L(−12)=−3kQ22L
Step 5: Relate to the Given Force F
From the problem, we know that the force F between any two charges is given by:
F=kQ2L2
We can express kQ2/L in terms of F:
kQ2L=F⋅L
Substituting this into the work done equation:
W=−32(F⋅L)
Final Answer
Thus, the work required to double the dimensions of the triangle is:
W=−32FL
We have three identical charges Q placed at the corners of an equilateral triangle with side length L. The force between any two charges is given as F.
The potential energy U between two point charges is given by the formula:
U=kQ1Q2r
For three identical charges at the corners of the triangle, the potential energy due to each pair of charges is:
Upair=kQ2L
Since there are three pairs of charges (between each pair of corners), the total initial potential energy Ui is:
Ui=3⋅kQ2L=3kQ2L
When the dimensions of the triangle are doubled, the new side length becomes 2L. The potential energy for each pair of charges in the new configuration is:
U′pair=kQ22L
The total final potential energy Uf is:
Uf=3⋅kQ22L=3kQ22L
The work done W by an external agent to change the configuration is equal to the change in potential energy:
W=Uf−Ui
Substituting the values we calculated:
W=3kQ22L−3kQ2L
To simplify, we can factor out 3kQ2L:
W=3kQ2L(12−1)=3kQ2L(−12)=−3kQ22L
From the problem, we know that the force F between any two charges is given by:
F=kQ2L2
We can express kQ2/L in terms of F:
kQ2L=F⋅L
Substituting this into the work done equation:
W=−32(F⋅L)
Thus, the work required to double the dimensions of the triangle is:
W=−32FL
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE
6 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
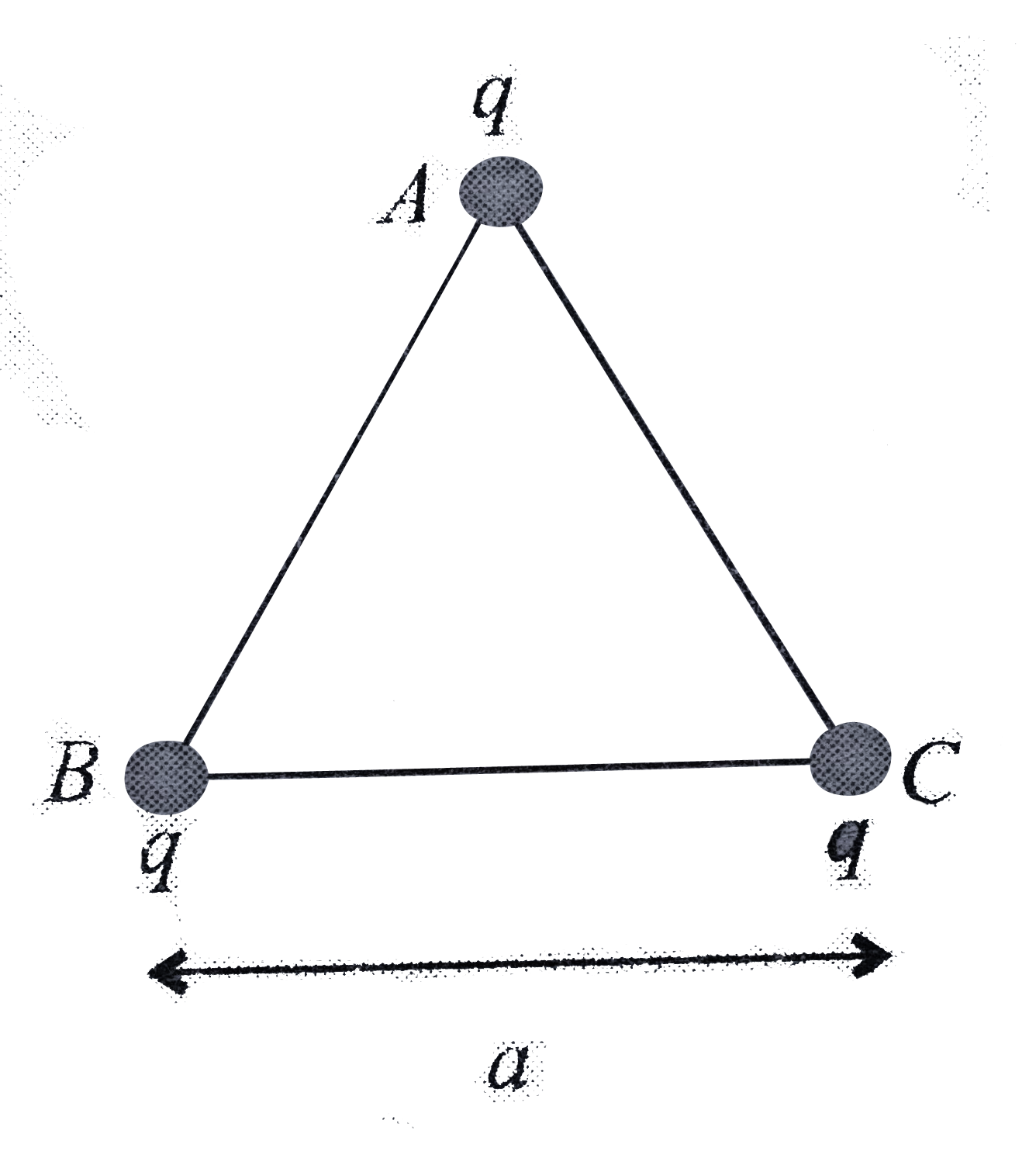
Three equal charges q are placed at the corners of an equilateral triangle of side A.
(i) Find out potential energy of charge system.
(ii) Calculate work required to decrease the side of triangle to a/2.
(iii) If the charges are released from the shown position and each of them has same mass m, then find the speed of each particle when they lie on triangle of side 2a.
 .
.
View SolutionThree equal charges q are placed at the corners of an equilateral triangle of side A.
(i) Find out potential energy of charge system.
(ii) Calculate work required to decrease the side of triangle to a/2.
(iii) If the charges are released from the shown position and each of them has same mass m, then find the speed of each particle when they lie on triangle of side 2a.
 .
.
View SolutionThree identical charges are placed at the vertices of an equilateral triangle. The force experienced by each charge, (if k=14πε0) is
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree equal charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out force acting on one of the charge due to other two charges ?
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionThree identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View SolutionThree point charges 1C,2C and 3C are placed at the corners of an equilaternal triangle of side 1m. The work required to move these charges to the corners of a smaller equilaternal triangle of side 0.5m in two differenct ways as in fig. (A) and fig. (B) are Wa and Wb then:

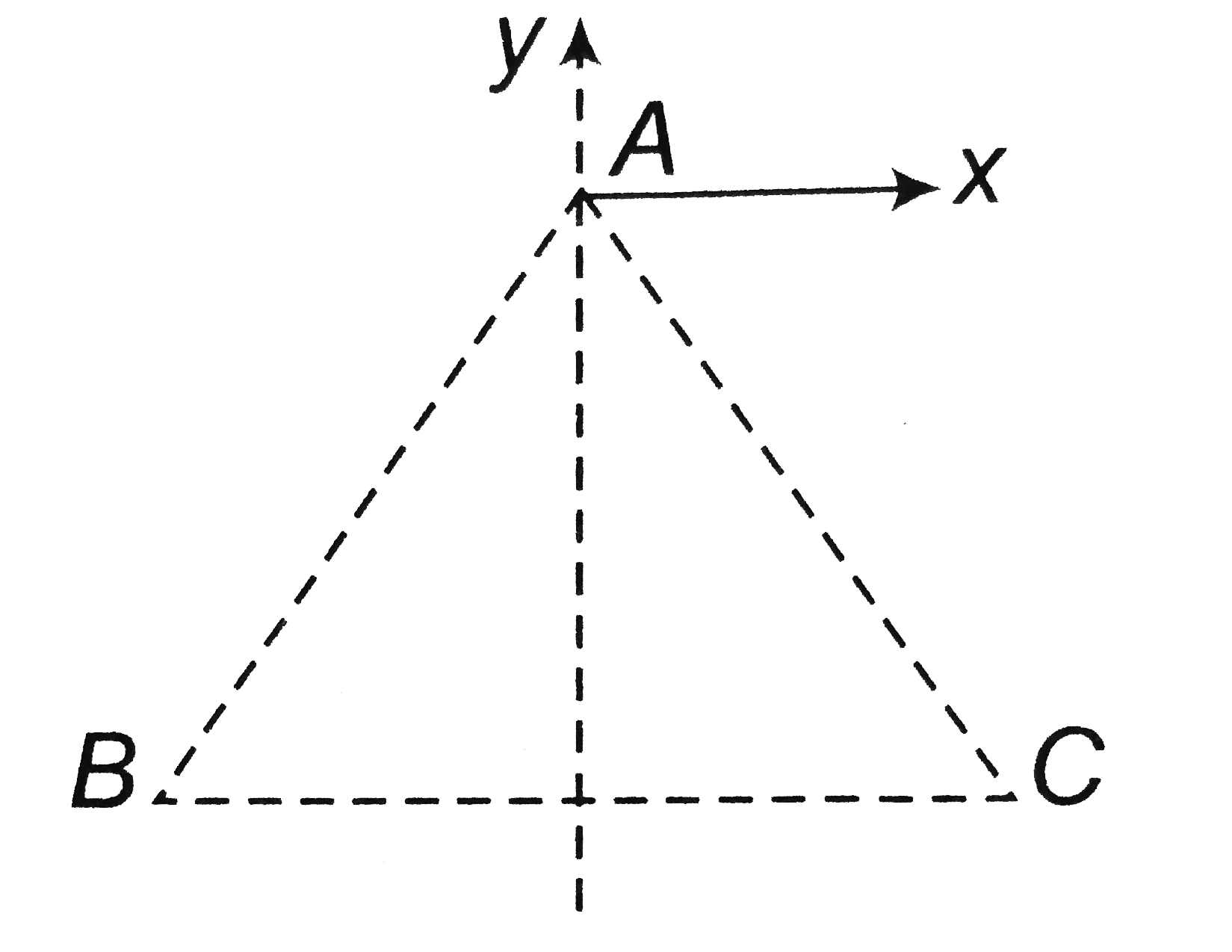
View SolutionThree similar charges +q are placed on 3 corners of an equilateral triangle ABC of side a. How many minimum charges should be placed on a circle of radius a with centre at A so that resultant force on the charge placed at the centre is q24πε0a2 along x-axis,
View Solution