Let A and B be two 2×2 matrices. Consider the statements (i) AB=0⇒A=0orB=0 (ii)AB=I2⇒A=B−1 (a) only (i) (b) only (ii) (c) both are correct (d) none of these.Solution in Bengali
Step by step video & image solution for Let A and B be two 2xx2 matrices. Consider the statements (i) A B=0 => A=0 or B=0 (ii)AB=I_2 => A=B^(-1) (a) only (i) (b) only (ii) (c) both are correct (d) none of these. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Statements -1 : ~(p↔~q) is equivalent to p↔q
Statement-2: ~(p↔~q) is a tautology.
View SolutionIf y=cos−1√√1+x2+12√1+x2,thendydxisequa<o 12(1+x2),x∈R (b) 12(1+x2),x>0 −12(1+x2),x<0 (d) 12(1+x2),x<0
View SolutionLet alpha and beta(alpha
View SolutionLet A,B be two matrices such that they commute, then for any positive integer n, ABn=BnA (AB)nAnBn only (i) and (ii) correct both (i) and (ii) correct only (ii) is correct none of (i) and (ii) is correct
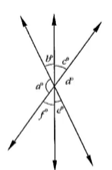
View SolutionIn Figure, which of the following statements must be true? (i) a+b=d+c (ii) a+c+e=1800 (iii) b+f=c+e (a) (i) only (b) (ii) only (c) (iii) only (d) (ii) and (iii) only
View SolutionIf A and B are two matrices such that AB=A and BA=B , then B2 is equal to (a) B (b) A (c) 1 (d) 0
View SolutionIf A and B are square matrices of order 3 then (A) AB=0→|A|=0or|B|=0 (B) AB=0→|A|=0and|B|=0 (C) Adj(AB)=AdjAAdjB (D) (A+B)−1=A−1+B−1
View SolutionIf A and B are any 2×2 matrices then det(A+B)=0 implies (A) detA+detB=0 (B) detA=0ordetB=0 (C) AB=0→|A|=0and|B|=0 (D) AB=0→A=0orB=0
View Solutionआव्यूह A तथा B एक दूसरे के व्युत्क्रम होंगे केवल यदि
(A) AB = BA
(B) AB = BA = 0
(C) AB = 0, BA = I
(D) AB = BA = I
View SolutionMatrices A and B will be inverse of each other only if (A) AB=BA(B) AB=BA=0(C) AB=0,BA=I(D) AB=BA=I
View SolutionLet A and B be two 2×2 matrices. Consider the statements (i) AB=0⇒A=0orB=0 (ii)AB=I2⇒A=B−1 (a) only (i) (b) only (ii) (c) both are correct (d) none of these.
View SolutionLet AandB be two 2×2 matrices. Consider the statements (i) AB=O⇒A=OorB=O (ii)AB=I2⇒A=B−1 (iii) (A+B)2=A2+2AB+B2 (a)(i) and (ii) are false, (iii) is true (b)(ii) and (iii) are false, (i) is true (c)(i) is false (ii) and, (iii) are true (d)(i) and (iii) are false, (ii) is true
View SolutionIn Figure, which of the following statements must be true?
(i) a+b=d+c
(ii) a+c+e=1800
(iii) b+f=c+e
(a) (i) only
(b) (ii) only
(c) (iii) only
(d) (ii) and (iii) only
View SolutionThe statement (a+ib)<(c+id) is true for a2+b2=0 (b) b2+d2=0 b2+c2=0 (d) None of these
View SolutionIf A and B are square matrices of order 3 then (A) AB=0→|A|=0or|B|=0 (B) AB=0→|A|=0and|B|=0 (C) Adj(AB)=AdjAAdjB (D) (A+B)−1=A−1+B−1
View Solution
