Question

Solve : $x^2=\left\{x\right\}$, where $\left\{x\right\}$ represents the fractional part function.

Explanation

We have `x^(2)= {x}`.
Draw the graphs of `y= x^(2) and y = {x}` to locate the points of intersection.

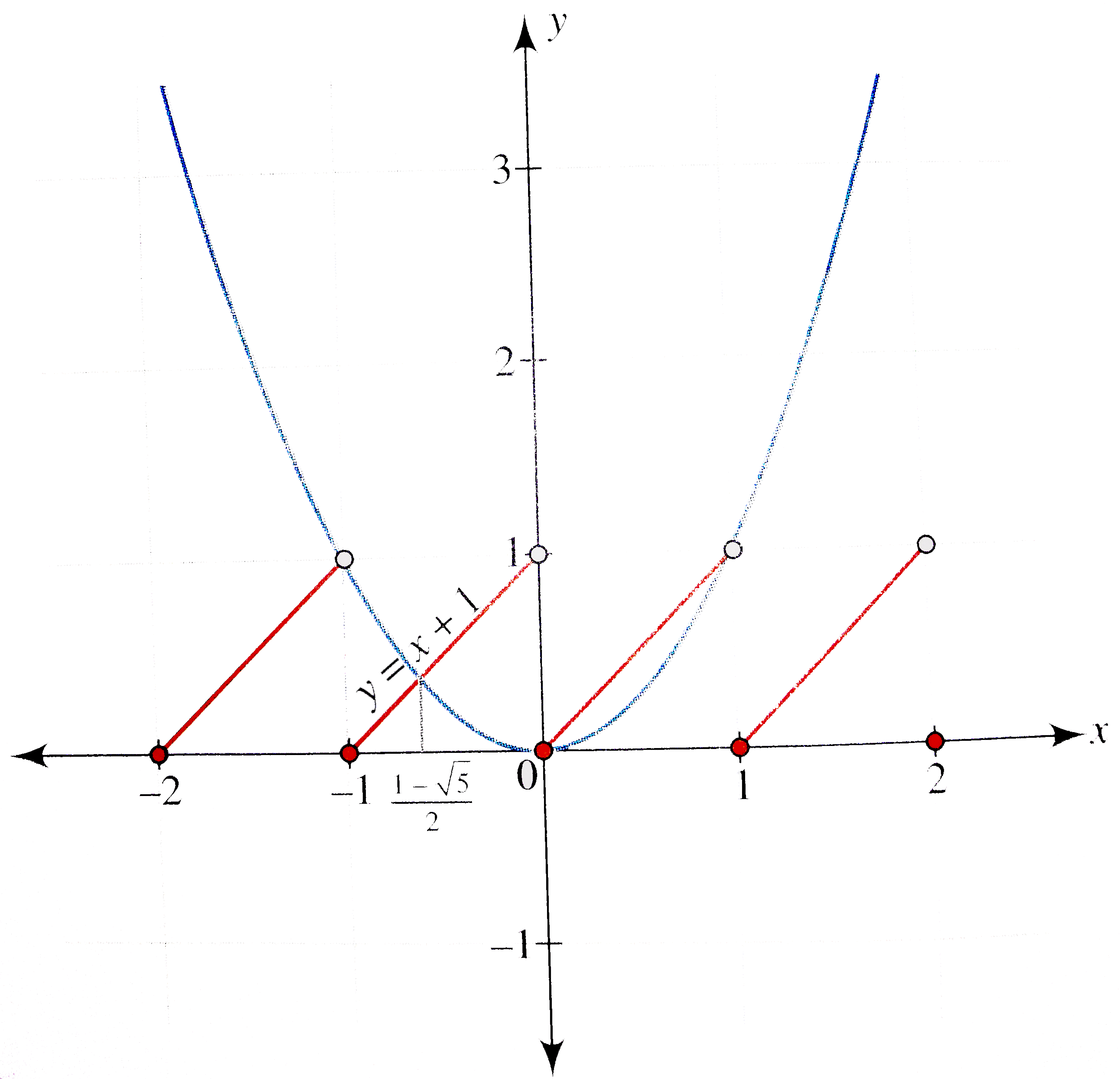
From the graphs, it is clear that one root is `x=0`
Both graphs intersect once in `x in (-1, 0)`.
Solving for this interval, we have `x^(2) = x+1 or x^(2) -x-1=0`.
`therefore " "x=(1-sqrt5)/(2)`
Hence the are two roots `x=0 and x= (1-sqrt5)/(2)`.