The equations of bisectors of two lines L1&L2 are 2x−16y−5=0 and 64x+8y+35=0. lf the line L1 passes through (−11,4), the equation of acute angle bisector of L1 & L2 is:Solution in Bengali
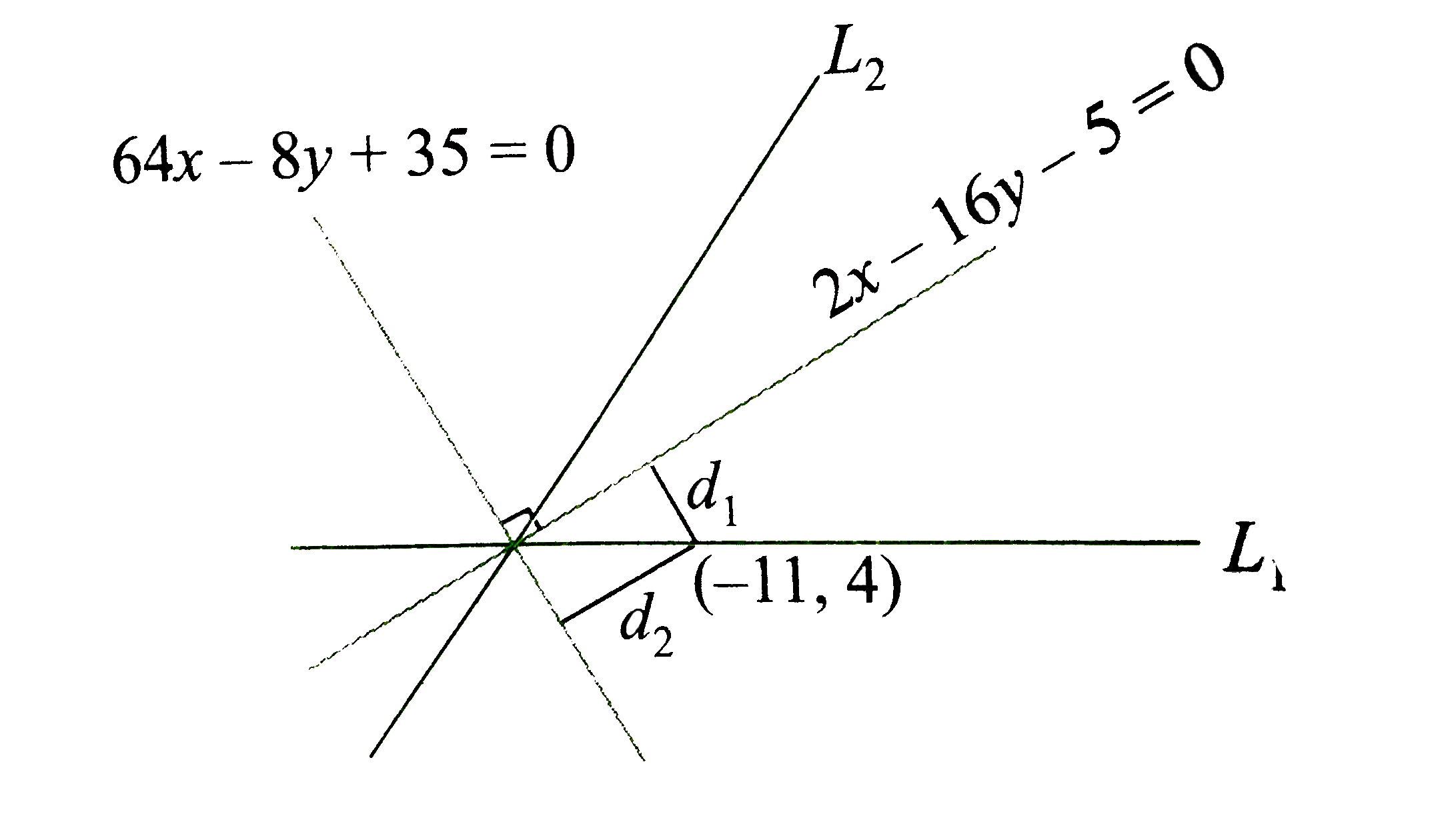
From the figure,
d1=|2(−11)−16(4)−5|√4+256=912√65≅5.6 (1)
d2=|64(−11)+8(4)+35|√(64)2+82=63764.49≅9.87 (2)
d1<d2
Therefore, 2x-16y-5=0 is acute angle bisector and 64x+8y+35=0 is obtuse angle bisector.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE12videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.123videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
Show that the lines 4x+y−9=0,x−2y+3=0,5x−y−6=0 make equal intercepts on any line of slope 2.
06:55View SolutionFind the equation of the right bisector of the line segment joining the points (3,4) and (-1,2).
04:38View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
03:09View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
02:38View SolutionThe equations of bisectors of two lines L_(1)&L_(2) are 2x-16y-5=0 and 64x+8y+35=0. lf the line L_(1) passes through (-11,4), the equation of acute angle bisector of L_(1)o*L_(2) is:
04:18View SolutionLet L_1 :x+y-3= 0 and L_2:7x -y +5 = 0 be two given lines. Let image of every point on L_1, with respect to a line L lies on L_2 then possible equation of L can be :
02:47View SolutionThe vector equations of two lines L1andL2 are respectively, L1:r=2i+9j+13k+λ(i+2j+3k)andL2:r=−3i+7j+pk+μ(−i+2j−3k) Then, the lines L1andL2 are
View SolutionIf line l1 is perpendicular to line l2 and line l3 has slope 3 then find the equation of line l1
 02:05View Solution
02:05View SolutionThe equations of bisectors of two lines L1&L2 are 2x−16y−5=0 and 64x+8y+35=0. lf the line L1 passes through (−11,4), the equation of acute angle bisector of L1 & L2 is:
03:21View Solutionθ1andθ2 are the inclination of lines L1andL2 with the x-axis. If L1andL2 pass through P(x1,y1), then the equation of one of the angle bisector of these lines is
04:59View SolutionL1:3x+4y+8=0,L2:2x+7y−1=0
Equation of the line through B parallel to AC is02:14View SolutionL1andL2 are two intersecting lines. If the image of L1 w.r.t. L2 and that of L2 w.r.t. L1 concide, then the angle between L1andL2 is
03:58View SolutionLet L1:3X+4Y−1=0andL2:5z−12y+2=0 be two given lines. Let image of every point on L1 w.r.t a line L lies on L2 then possible equation of 'L' can be
06:03View SolutionThe straight line L≡X+Y+1=0andL1≡X+2Y+3=0 are intersectiong, m is the slope of the straight line L2 such that L is the bisector of the angle between L1andL2 The value of m2 is .
01:33View SolutionPoints (3, 0) and (-1,0) are invariant points under reflection in the line L1 points (0, -3) and (0, 1) are invariant points on reflection in line L2
Name or write equations for the lines L1 and L202:40View SolutionThe vector equations of two lines L1andL2 are respectively, L1:r=2i+9j+13k+λ(i+2j+3k)andL2:r=−3i+7j+pk+μ(−i+2j−3k) Then, the lines L1andL2 are
05:56View Solution

