
A rod AB is moving on a fixed circle of radius R with constant velocity as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
(i) Find the speed of point of intersection P.
(b) Find the angular speed of point of intersection P with respect to centre of the circle.Solution in Bengali
The correct Answer is:14x+23y-40=0
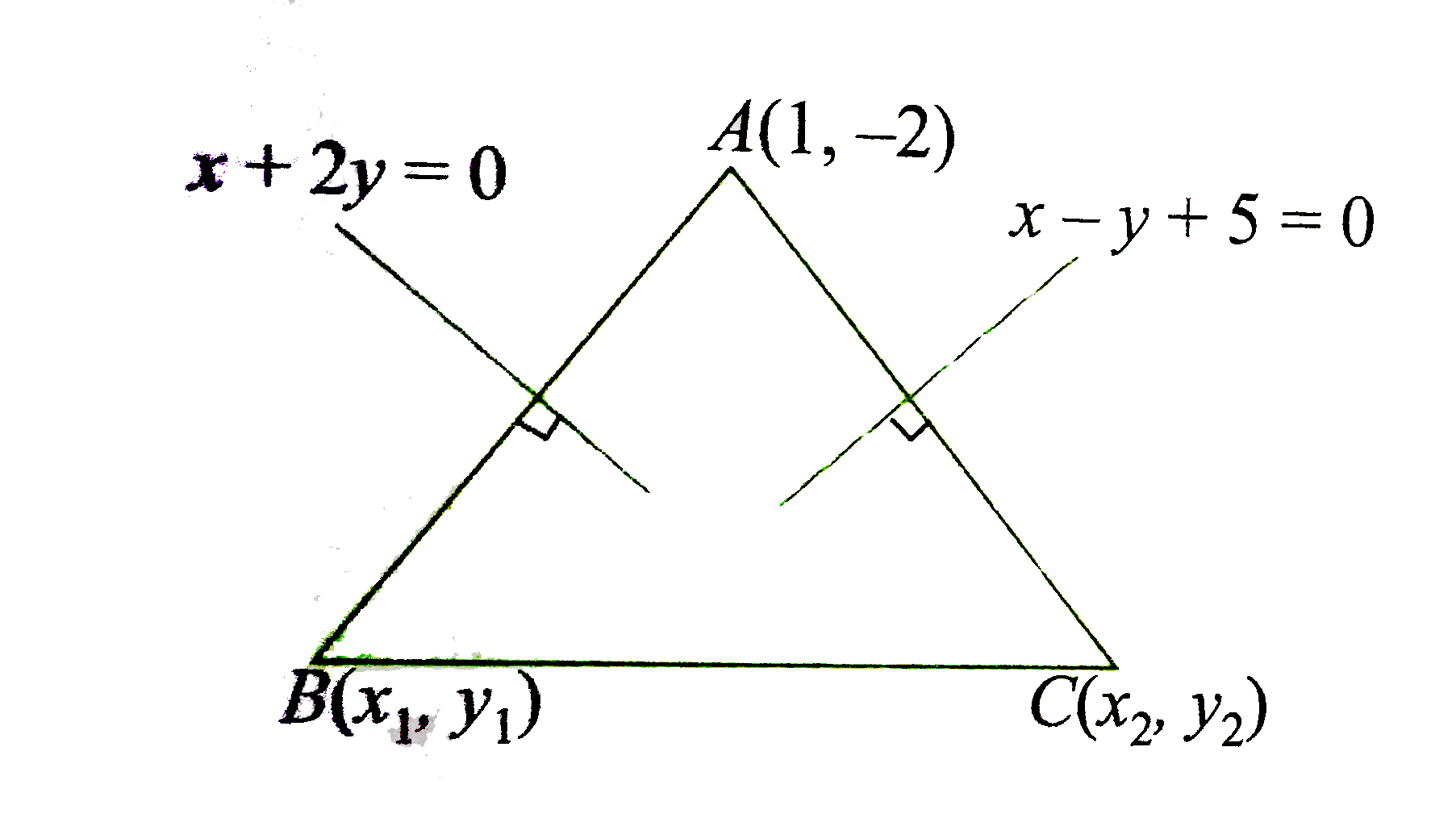
Since the given lines are perpendicular bisectors of the sides as shown in the figure, point B and C are the images of the point A in these lines. Therefore,
Hence, the line passing through the points B and C is 14x+23y-40=0.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (SINGLE CORRECT ANSWER TYPE)82videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.48videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
If aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
04:49View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
03:30View SolutionThe point (8,−9) with respect to the lines 2x+3y−4=0 and 6x+9y+8=0 lies on
01:34View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
04:40View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
02:49View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2 ms^-1 towards right. The velocity of end B of rod at the instant shown in figure is
View SolutionA rod AB is shown in figure. End A of the rod is fixed on ground. Block is moving with velocity m/s towards right. The velocity of end B of rod when rod makes an angle of 60^@ with ground is :
02:44View SolutionTwo points of a rod move with velocity 3 v and v perpendicular to the rod and in the same direction. Separated by a distance r . Then the angular velocity of the rod is :
05:25View SolutionA rod AB is moving on a fixed circle of radius R=5m with constant velocity v=4m//s as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=(3R)/5 from center of the circle. The velocity of the rodf is perpendicular to its lenght and the rod is always paraller to the diameter (CD) Speed of point of intersection P is
01:42View SolutionA rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=(3R)/(5) from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD . (a) Find the speed of point of intersection P (b) Find the angular speed of point of intersection P with respect to centre of the circle.
05:01View SolutionThere is a fixed half cylinder of radius R on a horizontal table. A uniform rod of length 2R leans against it as shown. At the instant shown, θ=30∘ and the right end of the rod is sliding with velocity v.
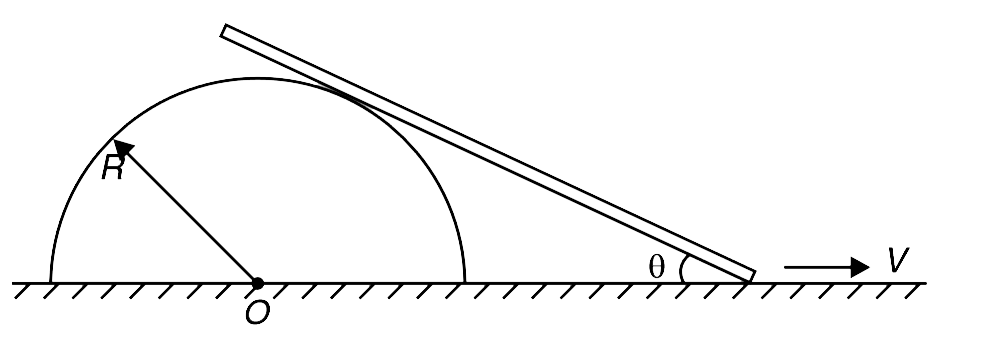
(a) Calculate the angular speed of the rod at this instant.
(b) Find the vertical component of the velocity of the centre of the rod at this instant.02:50View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R03_E09_002_Q01.png" width="80%"gt
01:35View SolutionA rod AB is placed on smooth inclined plane as shown in the figure. At the instant which is shown in the figure, the angular velocity of the rod is
04:03View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2 ms^-1 towards right. The velocity of end B of rod at the instant shown in figure is
02:19View SolutionA rod AB of weight w_(1) is placed over a sphere of weight w_(2) shown in figure.Ground is rough and there is no friction between rod and sphere and sphere and wall. Draw free body diagram of sphere and rod separately.
04:19View Solutionएक छड़ के दो बिन्दु, छड़ के लम्बवत समान दिशा में 3v तथा v वेग से गति करते हैं। दोनो बिन्दु एक दूसरे से .r. दूरी पर हैं तो छड़ का कोणीय वेग होगा :
03:11View Solution

