The equation of a line through the point (1, 2) whose distance from the point (3,1) has the greatest value is (a)y=2x (b)y=x+1 (c)x+2y=5 (d) y=3x−1Solution in Bengali
y=2x
y=x+1
x+2y=5
y=3x-1
The correct Answer is:A
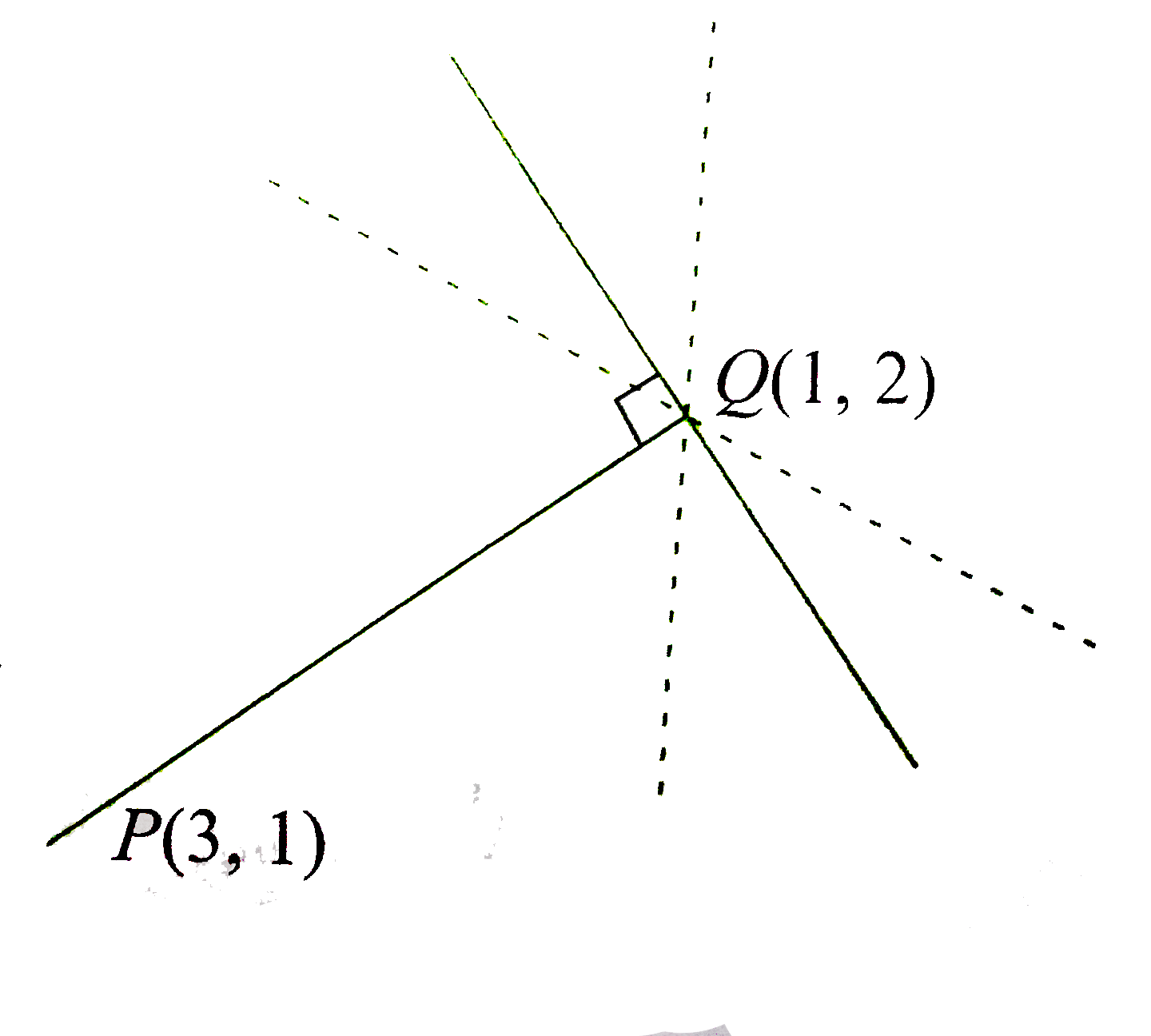
Obviously, the line through Q is at the greatest distance from point P when it is perpendicular to PQ. Now, the slope of line PQ is mPQ=−1/2. Then the slope of perpendicular line passing through Q is
y-2 = 2(x-1)
or 2x-y=0
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionFind the distance of the point on y=x4+3x2+2x which is nearest to the line y=2x−1
View SolutionThe equation of the bisector of the acute angle between the lines 2x−y+4=0 and x−2y=1 is (a) x−y+5=0 (b)x−y+1=0 (c)x−y=5 (d) none of these
View SolutionFind the equation to the line passing through the point of intersection of y-x-1=0 and 2x-y+1=0 and perpendicular to 3x+2y=0
View SolutionThe equation of the curve passing through origin, whose slope at any point is x(1+y)1+x2, is (A) (1+y)2−x2=1 (B) x2+(y+1)2=1 (C) (x+y)y=1−x2 (D) x=ye(1+y)
View Solutiony=2(x−1) और y=3x−5 के प्रतिच्छेद बिन्दु से होकर जाने वाली उस रेखा का समीकरण ज्ञात कीजिए, जिसकी मुलबिन्दु से दुरी 7√2 मात्रक है।
View Solutionउस रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,1) से तथा रेखाओं x+y−1=0 और 3x+2y+1=0 के प्रतिच्छेद बिन्दुओं से होकर जाती है।
View Solutionरेखाओ 2x+y=1 और 3x−y+5=0 के प्रतिच्छेद बिंदु से होकर जाने वाले उस रेखा का समीकरण ज्ञात कीजिये , जो 3x−2y=0 के समांतर है
View SolutionThe equation of a line through the point (1, 2) whose distance from the point (3, 1) has the greatest possible value is :
View SolutionFind the distance of the point on y=x4+3x2+2x which is nearest to the line y=2x−1
View SolutionThe equation of the bisector of the acute angle between the lines 2x−y+4=0 and x−2y=1 is (a) x−y+5=0 (b)x−y+1=0 (c)x−y=5 (d) none of these
View SolutionThe point of intersection of the line passing through (0,0,1) and intersecting the lines x+2y+z=1,−x+y−2z=2 and x+y=2,x+z=2 with xy plane is a. (53,−13,0) b. (1,1,0) c. (23,13,0) d. (−53,13,0)
View Solution
