Doubtnut Promotions Sticky

Draw the graph of y=tan−1(2x1−x2)Solution in Bengali

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We have y=f(x)=tan−1(2x1−x2)
Domain of f(x) is R-{-1, 1}.
Let x=tanθ∈(−π/2,π/2)
⇒ θ=tan−1x
Now tan−1(2x1−x2)=tan−1(2tanθ1−tan2θ)
=tan−1(tan2θ)
=tan−1(tanα) where α∈(−π,π)
Now consider the graph of y=tan−1(tanα), where α∈(−π,π).
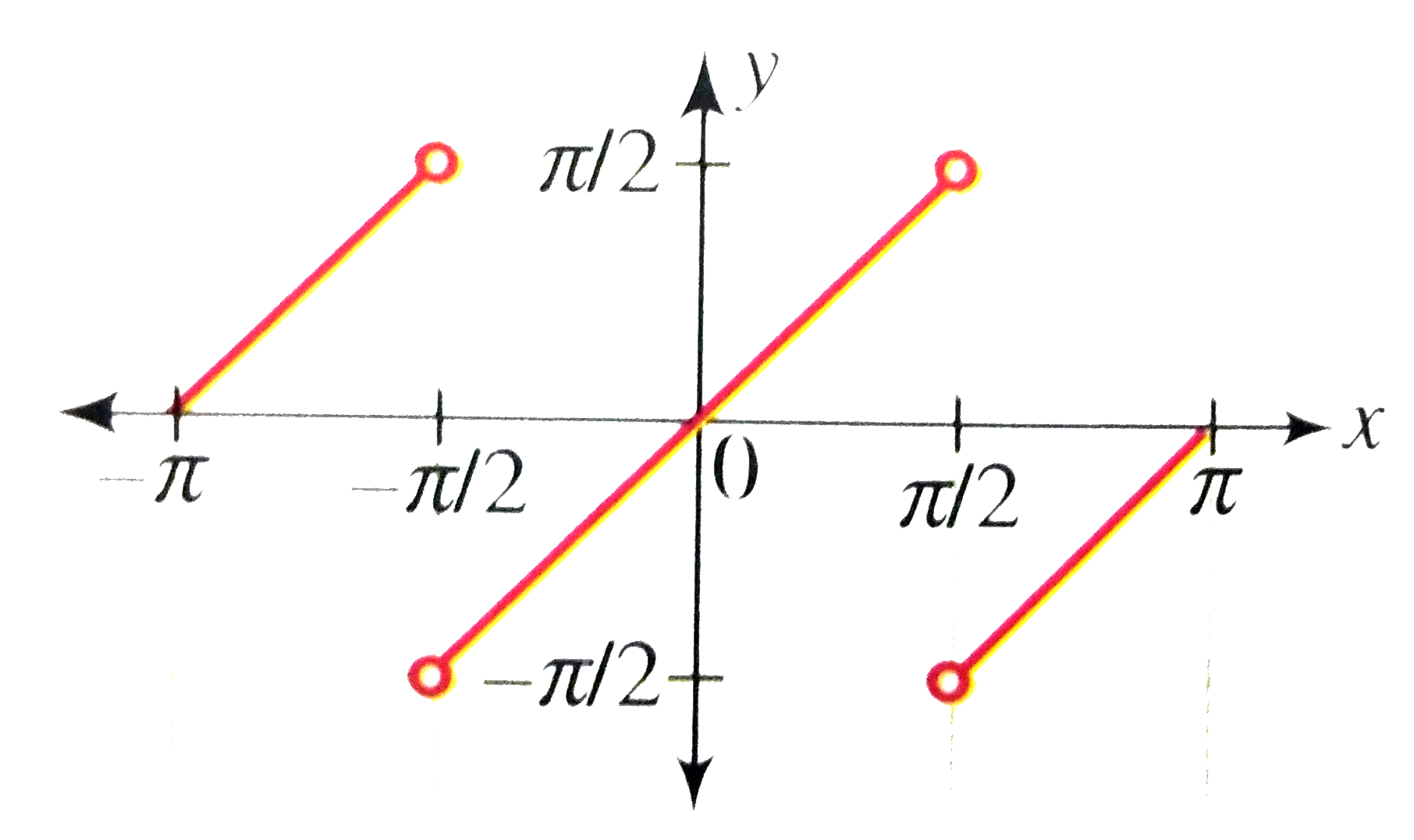
ocr_image
Form the graph,
tan−1(2x1−x2)=tan−1(tanα)
=⎧⎪⎨⎪⎩α+π−π<α<−π/2α−π/2<α<π/2α−ππ/2≤α<π
=⎧⎪ ⎪⎨⎪ ⎪⎩2tan−1x+π−π<tan−1x<−π/22tan−1x−π/2<tan−1x<π/22tan−1x−ππ/2<2tan−1x<π
=⎧⎪ ⎪⎨⎪ ⎪⎩2tan−1x+π−π<tan−1x<−π/42tan−1x−π/4<tan−1x<π/42tan−1x−ππ/4<2tan−1x<π/2
=⎧⎪⎨⎪⎩2tan−1x+π−∞<x<−12tan−1x−1<x<11tan−1x−π1<x<∞
tan−1 is an increasing function for x∈R.
Thus, all branch functions in the above are increasing functions.
limx→−∞(tan−1x+π)=0,limx→−1(2tan−1x+π)=π2
Thus, tan−1(2x1−x2) increases form 0 to π2 when x increases from −∞ to −1
limx→−1(2tan−1x)=π2,limx→1(2−1limx)−π2 and 2tan−10=0
Thus, tan−1(2x1−x2) increases form −π2 to π2 when x increases from -1 to 1, intersecting the x-axis at x=0.
limx→1(2tan−1x−[π)=−π2,limx→∞(2tan−1x−π)=0
Thus, tan−1(2x1−x2) increases form −π2 to0 when x increases from 1 to ∞.
From this information, we can draw the graph of y=tan−1(2x1−x2) as folows.
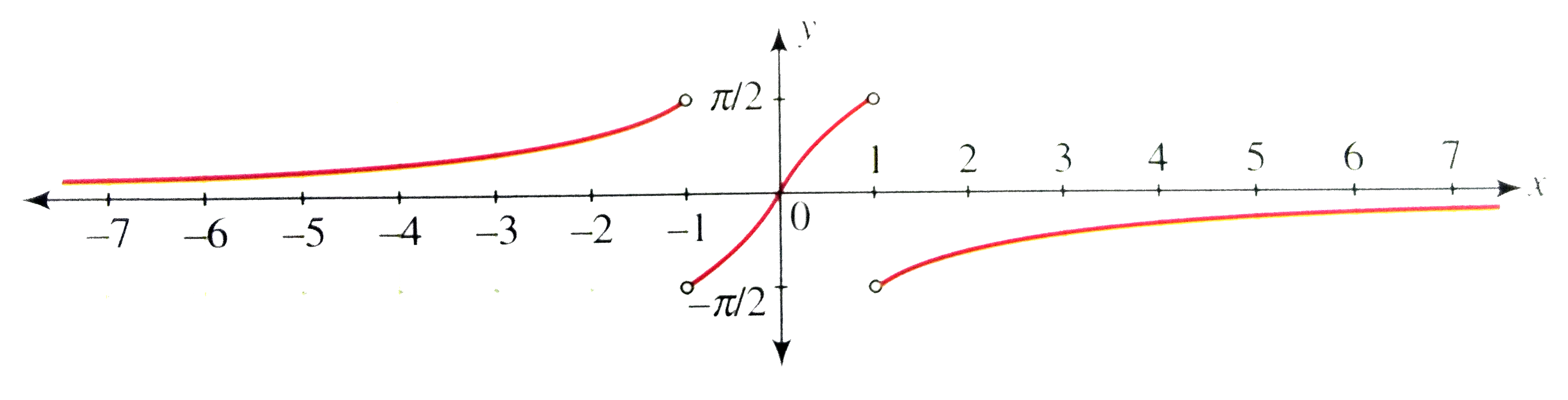
ocr_image
Here y = 0 is na anymptote.

|
Updated on:21/07/2023
Class 12MATHSINVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions