The point at which the tangent to the curve $y = x^{2} - 4 x$ is parallel to x-axis is

A

$(0, 4)$

B

$(- 2, 4)$

C

$(2, 4)$

D

$(2, - 4)$

Text Solution

Verified by Experts

The correct Answer is:A

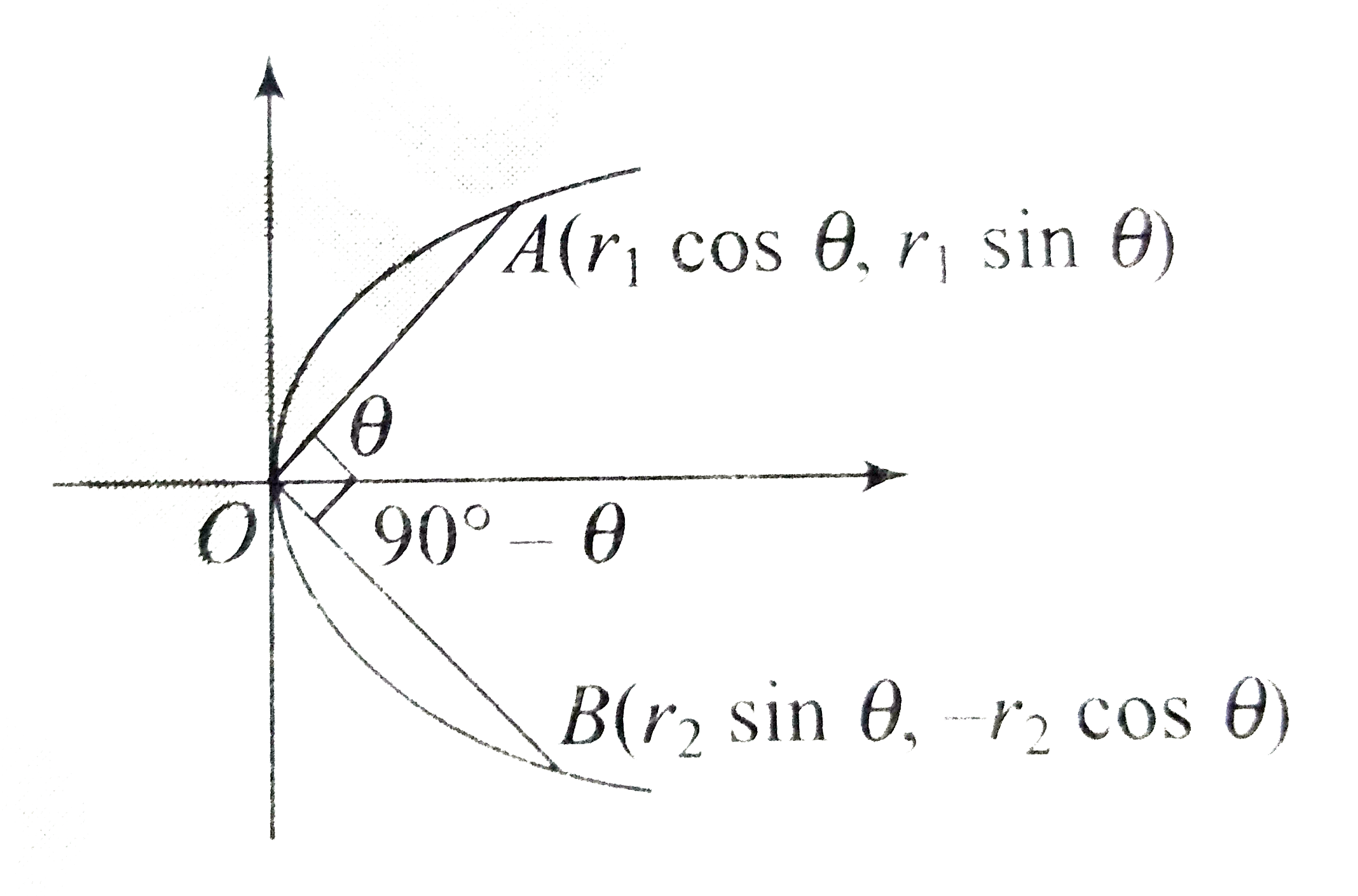
$r_{1}^{2} {sin}^{2} θ = 4 a r_{1} cos θ$ (i)
and $r_{2}^{2} {cos}^{2} θ = 4 a r_{2} sin θ$ (ii)
From Eq. (i), we get $r_{1}^{2} {sin}^{4} θ = 16 a^{2} {cos}^{2} θ$ (iii)
from Eqs. (ii) and (iii), we get
${sin}^{3} θ = \frac{64 a^{3}}{r_{1}^{2} r_{2}}$ (iv)
similarly, ${cos}^{3} θ = \frac{64 a^{3}}{r_{1} r_{2}^{2}}$
Eliminating $θ$ , we get
$\frac{r_{1}^{4 / 3} r_{2}^{4 / 3}}{r_{1}^{2 / 3} + r_{2}^{2 / 3}} = 16 a^{2}$

|

Updated on:21/07/2023

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The point on the curve $y = x^{3}$ at which the tangent to the curve is parallel to the X-axis, is
A $(2, 2)$
B $(3, 3)$
C $(4, 4)$
D $(0, 0)$
Question 2 - Select One
The tangent to the curve $x^{2} + y^{2} - 2 x - 3 = 0$ is parallel to X-axis at the points
A $(2, \pm \sqrt{3})$
B $(1, \pm 2)$
C $(\pm 1, 2)$
D $(\pm 3, 0)$

CENGAGE PUBLICATION-PARABOLA-Single Correct Answer Type

Home
Ask Doubt
Profile