The circle x2+y2=4cuts the line joining the points A(1,0) and B(3,4) in two points P and Q. Let BPPA=α and BQQA=β. Then α and β are roots of the quadratic equation
3x2−16x+21=0
x2−8x+7=0
x2−9x+8=0
none of these
The correct Answer is:1
The equation of the line joining A(1,0) and B(3,4) is y=2x−2
This cuts the circle x2+y2=4 at Q(0,−2) and P(8/5,6/5). We have BQ=3√5,QA=√5,BP=7√5 and PA=3√5 . Therefore,
α=BPPA=7√53√5=73
and β=BQQA=3√5√5=3
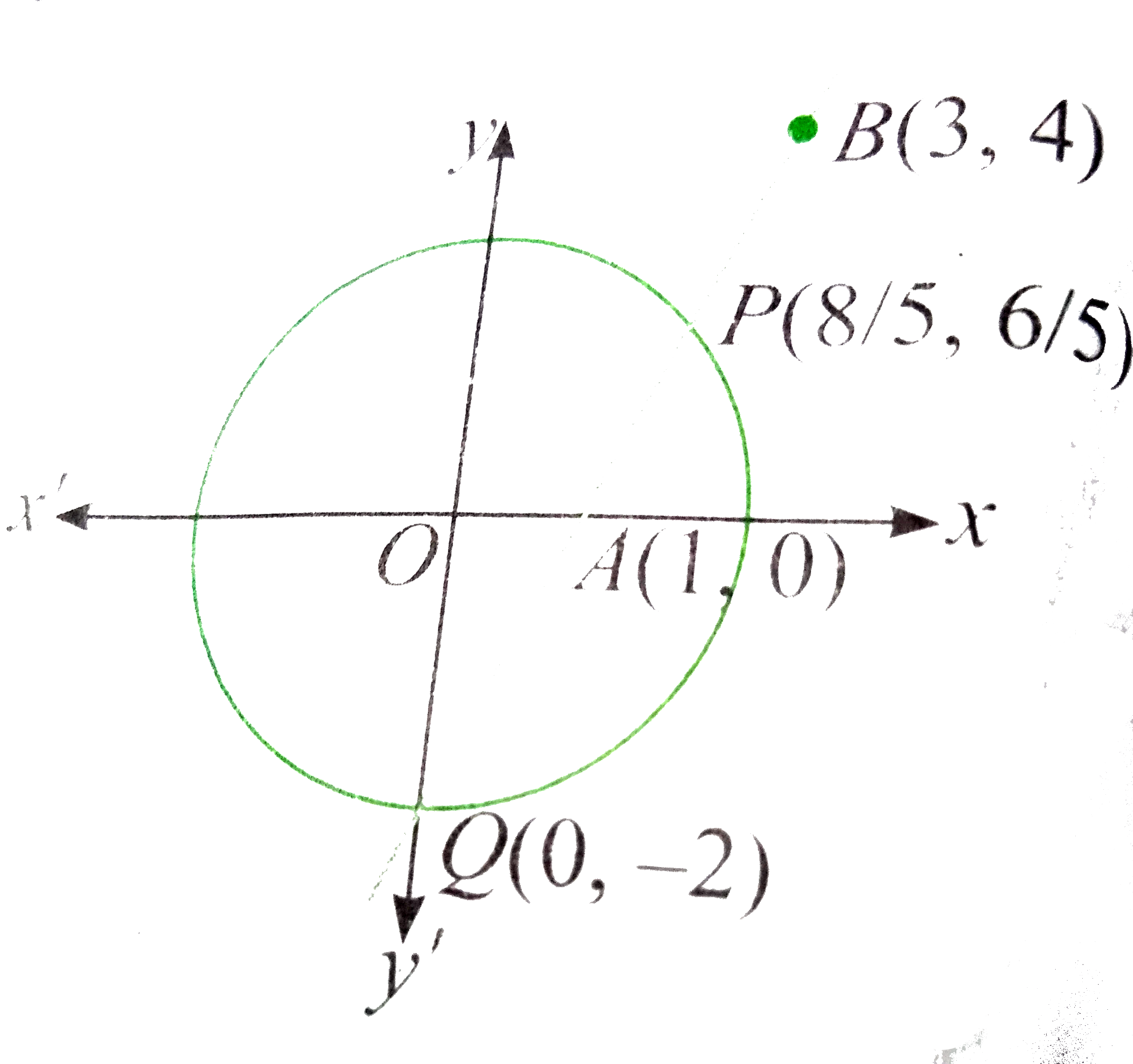
Therefore, α and β are roots of the equation
x2−x(alph+β)+αβ=0
i.e., x2−x(73−3)+73(3)=0
or 3x2−16x+21=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.17
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
The circle x2+y2=4cuts the line joining the points A(1,0) and B(3,4) in two points P and Q. Let BPPA=α and BQQA=β. Then α and β are roots of the quadratic equation
View SolutionThe circle x2+y2=4 ,cuts the line joining the points A(1,0),&B(3,4) in two points P& Q.Let BPPA=α>0&BQQA=β>0 .Then α+β
View Solution
Knowledge Check
If α and β are the roots of the quadratic equation 3m2+2m−4=0, then α2+β2=
A289B−289C129D−129
If the circles described on the line joining the points (0,1) and (α,β) as diameter cuts the axis of the points whose abscissae are the roots of the equation x2−5x+3=0 then (α,β)=
View SolutionIf α,β are the roots of the quadratic equation 4x2−4x+1=0 then α3+β3=
View Solutionif α,β roots of quadratic equation 2x2+3x−4=0 then find α+β
View SolutionIf α and β are the roots of the quadratic equation x2−3x−2=0, then αβ+βα=
View SolutionIf 2x+3y+4=0 is perpendicular bisector of the segment joining the points A(1,2) and B(α,β) then the value of α+β is
View SolutionIf the circles described on the line joining the points (0, 1) and (α,β) as diameter cuts the X-axis in points whose abscissae are roots of equation x2−5x+3=0 then (α,β) =
View SolutionIf α and β are the roots of a quadratic equation such that α+β=2,α4+β4=272 , then the quadratic equation is
View Solution
