From a point R(5, 8) two tangents RP and RQ are drawn to a given circle s=0 whose radius is 5. If circumcentre of the triangle PQR is (2, 3), then the equation of circle S = 0 isSolution in Bengali
The correct Answer is:1
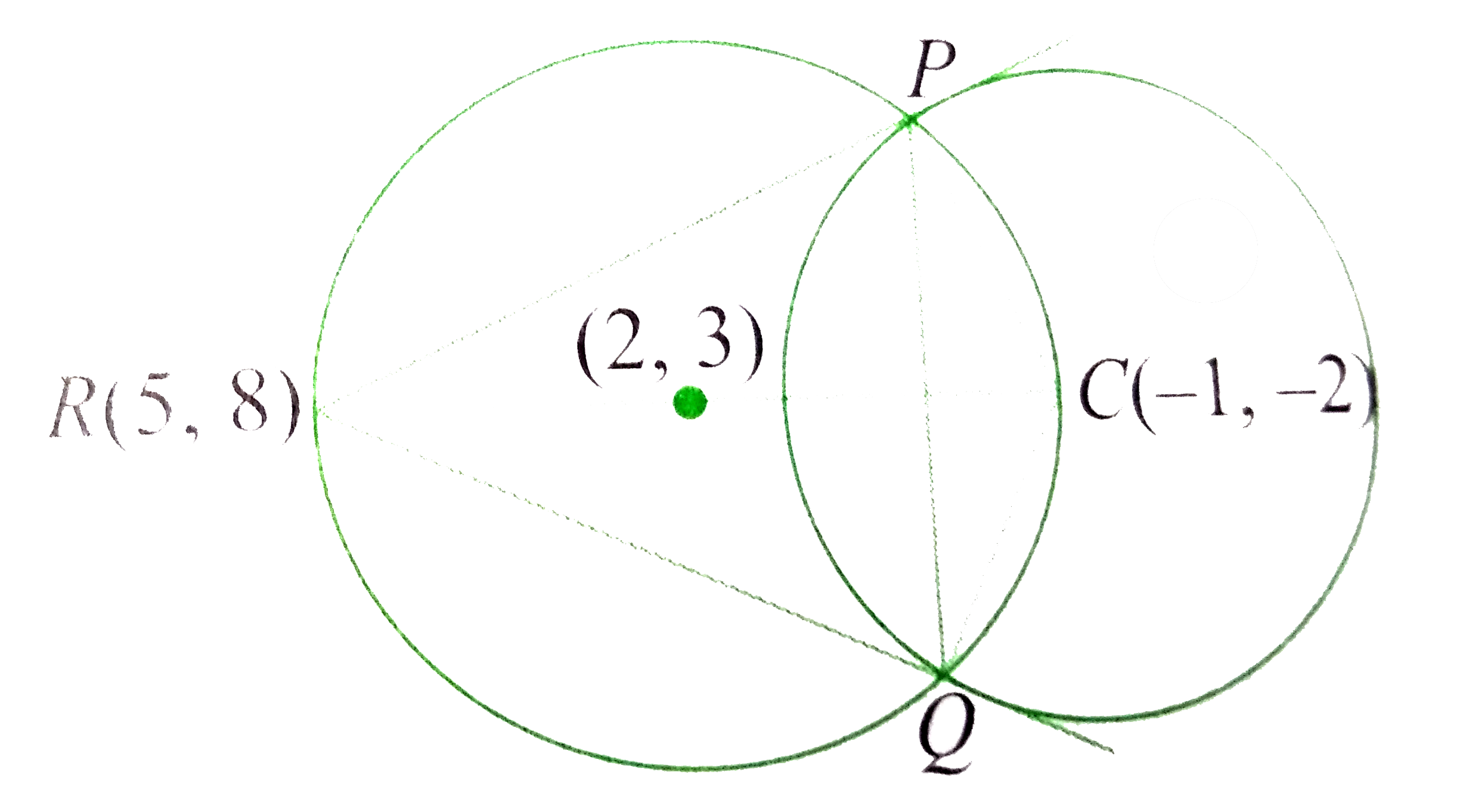
Let C be the center of the given circle.
Then, the circumcircle of passes through C.
Therefore, (2,3) is the midpoint of RC.
Thus, the coordinates of C are .
Hence, the equation of the circle is
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.17
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionThree concentric circles of which the biggest is x2+y2=1, have their radii in A.P If the line y=x+1 cuts all the circles in real and distinct points. The interval in which the common difference of the A.P will lie is:
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View Solutiontwo tangents RQ and RP are drawn from an external point R to the circle with centre O.If /_PRQ=120^(@), then prove that OR=PR+RQ
View SolutionFrom a point R(5,8) , two tangents RPandRQ are drawn to a given circle S=0 whose radius is 5. If the circumcenter of triangle PQR is (2, 3), then the equation of the circle S=0 is x2+y2+2x+4y−20=0 x2+y2+x+2y−10=0 x2+y2−x+2y−20=0 x2+y2+4x−6y−12=0
View SolutionFrom a point R(5, 8) two tangents RP and RQ are drawn to a given circle s=0 whose radius is 5. If circumcentre of the triangle PQR is (2, 3), then the equation of circle S = 0 is
View SolutionTangents are drawn from points on the line x+2y=8 to the circle x^(2)+y^(2)=16. If locus of mid-point of chord of contacts of the tangents is a circles S, then radius of circle S will be
View SolutionTwo tangents are drawn from any point P on a given line L=0 to a given circle S=0, if these tangents touch the circle at point A and B, then locus of the circumcentre the ΔPAB will be
View Solutionएक बिंदु जिसकी वृत्त के कन्द्र से दूरी 5 सेमी है, तथा वृत्त की त्रिज्या 3 सेमी है, से वृत्त पर खींची गयी स्पर्श रेखा की लम्बाई ज्ञात कौजिए।
View SolutionIf the equation fo two circles whose radii are a, a ' are S = 0 and S′=0, then show that circles Sa+S′a′=0andSa−S′a'=0 intersect orthogonally.
View SolutionA circle S=0 with radius √2 touches the line x+y-2=0 at (1,1). Then the length of the tangent drawn from the point (1,2) to S=0 is
View SolutionTwo tangents OP & OQ are drawn from origin to the circle x2+y2−x+2y+1=0 then the circumcentre of ΔOPQ is
View SolutionIf a circle S with radius 5 touches the circle x2+y2−6x−4y−12=0 at (-1,-1) , then the length of the tangent from the centre of the circle S to the given circle is
View SolutionThe equation to the side "BC" of "ΔABC" is "x+5=0" .If "(−3,2)" is the orthocentre and "(0,0)" is the circumcentre then radius of the circle is
View Solution
