(6,0),(0,6)and(7,7) are the vertices of a triangle. The circle inscribed in the triangle has the equation
x2+y2−9x−9y+36=0
x2+y2+9x−9y+36=0
x2+y2+9x+9y−36=0
x2+y2+18x−18y+36=0
The correct Answer is:2
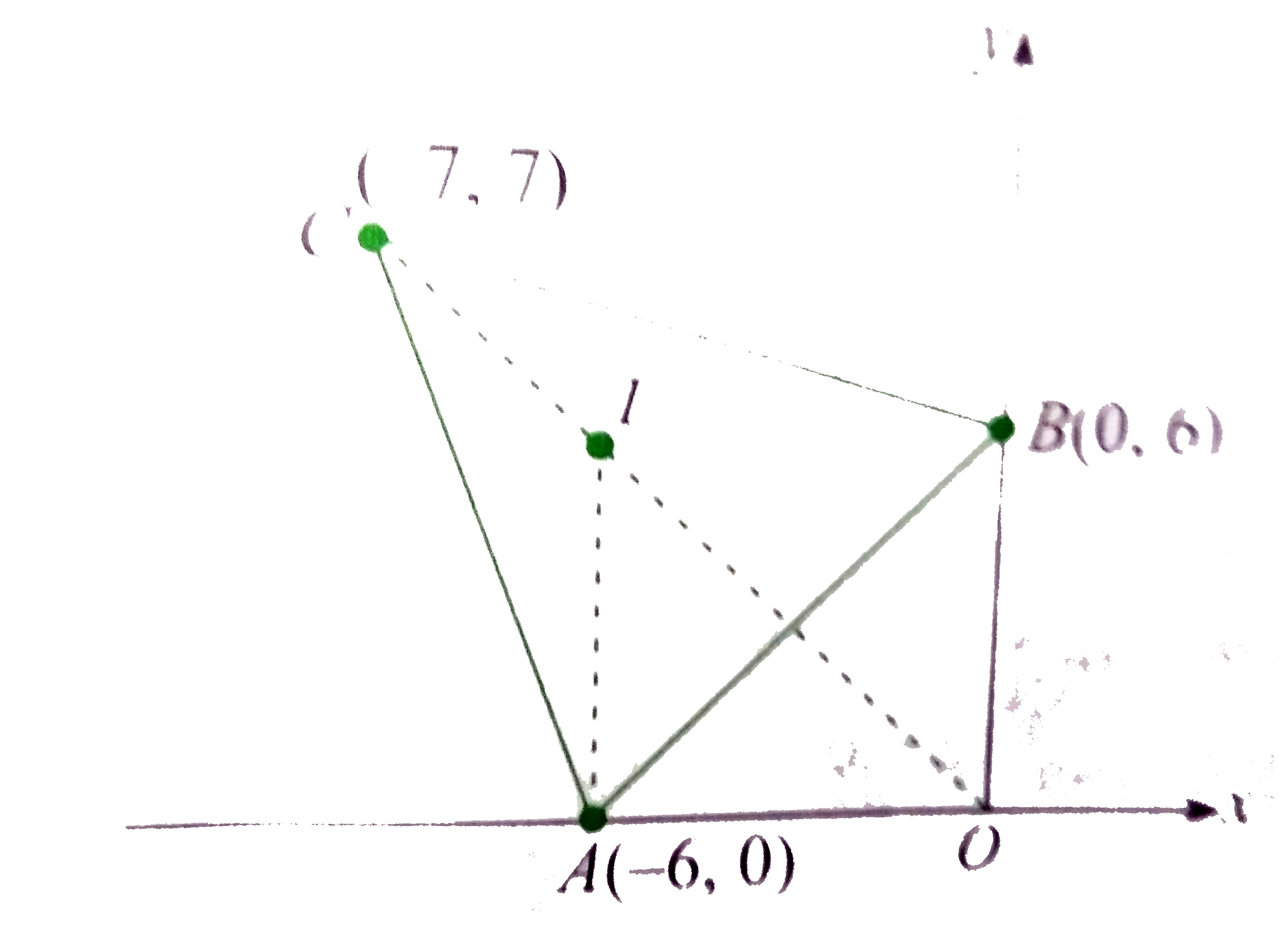
The triangle is evidently isosceles and, therefore, the median through C is the angle bisector of ∠C.
The equation of the angle bisector is y=−x and the incenter
I≡(−a,a) where a is positive.
The equation of AC is y−0=−7(x+6),i.e.,7x+y+42=0
and the equation of AB is x−y+6=0.
The lengths of the perpendiculars from I to AB and AC are equal. Therefore,
∣∣∣−7a=a+42√50∣∣∣=∣∣∣−a−a+6√2∣∣∣
or a=92 (∵a>0)
Therefore, the center is (−9/2,9/2) and the radius is 3/√2.
Hence, the equation of the circle is
(x+92)2+(y−92)2=92
or x2+y2+9x−9y+36=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.17
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Let A(0,2),B(3,0),C(6,4) be the vertices of triangle and P is a point inside the triangle such that area of triangle APB, BPC and CPA are equal. Equation of circle circumscribing ΔAPB is :
View SolutionIf midpoints of the sides of a triangle are (0, 4), (6, 4) and (6, 0), then find the vertices of triangle, centroid and circumcentre of triangle.
View Solution
Knowledge Check
The vertices of a triangle ABC are the points (6,0),(0,6) and (7,7). The equation of the circle inscribed in the triangle is
Ax2+y2−9x−9y+36=0Bx2+y2−9x−9y−36=0Cx2+y2−9x+9y+36=0Dx2+y2+9x−9y+36=0Let A(0,2),B(3,0),C(6,4) be the vertices of triangle and P is a point inside the triangle such that area of triangle APB, BPC and CPA are equal. Equation of circle circumscribing ΔAPB is :
Ax2+y2−2x−3y=0Bx2+y2−4x−3y=0Cx2+y2−3x−4y=0Dx2+y2−3x−2y=0If A (0, 7, 10), B(-1, 6, 6) and C(-4, 9, 6) are the vertices of ΔABC, then ΔABC is right angled at vertex
AABBCCDeither A or C
Show that the points (0,7,10),(−1,6,6)and(−4,9,6) are the vertices of as right angled triangle
View Solution(0,0) is the centre of the circle passing through the vertices of an equilateral triangle. If the length of the median of the triangle is 9 units then equation of the circle is
View SolutionVerify the following:(i) (0,7,10), (1,6,6)and (4,9,6)are the vertices of an isosceles triangle.
View SolutionFind the coordinates of the centreof the circle inscribed in the triangle whose vertices are (7,−36),(7,20) and (−8,0)
View SolutionIf coordinates of the vertices A, B, C of a triangle ABC are (6, 0), (0, 6) and (7, 7) respectively, then centre of the circle touching AB externally and BC and CA produced is
View Solution
