The ends of a quadrant of a circle have the coordinates (1, 3) and (3, 1). Then the center of such a circle is (2, 2) (b) (1, 1) (c) (4, 4) (d) (2, 6)Solution in Bengali
(2,2)
(1,1)
(4,4)
(2,6)
The correct Answer is:2
If (α,β) is the center, then
(α−1)2+(β−3)2=(α−3)2+(β−1)2 (1)
and β−3α−1.β−1α−3=−1
or (α−1)(α−3)+(β−1)(β−3)=0 (2)
From (1),
4α−4β=0
∴α=β
From (2),
2(α−1)(α−3)=0
∴α=1,3
∴(α,β)≡(1,1),(3,3)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type29videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)3videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.172videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
about to only mathematics
03:11View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
03:51View SolutionThree concentric circles of which the biggest is x2+y2=1, have their radii in A.P If the line y=x+1 cuts all the circles in real and distinct points. The interval in which the common difference of the A.P will lie is:
02:21View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is03:37View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is03:30View SolutionThe equation of the circle which touches the axes of coordinates and the line x3+y4=1 and whose center lies in the first quadrant is x2+y2−2cx−2cy+c2=0 , where c is (a) 1 (b) 2 (c) 3 (d) 6
07:36View Solutionकिसी वृत्त के एक व्यास के एक छोर के निर्देशांक (4, -1) हैं तथा वृत्त के केन्द्र के निर्देशांक (1, -3) हैं, तो व्यास के दूसरे छोर के निर्देशांक हैं -
03:27View Solutionकिसी वृत्त के केंद्र के निर्देशांक (−2,−3) है । यदि इसके व्यास AB के सिरे A के निर्देशांक (−1,4) हों , तो सिरे B के निर्देशांक ज्ञात कीजिए ।
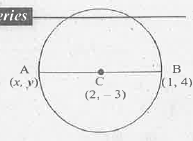
04:54View SolutionFind the coordinates of the point A, while AB is the center of the circle (2, -3) and B (1, 4).
05:30View SolutionAB ವ್ಯಾಸವಾಗಿರುವ ವೃತ್ತದ ಕೇಂದ್ರ (2, -3) ಮತ್ತು B ಯು (1, 4) ಆದರೆ, A ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
 01:36View Solution
01:36View Solutionদেখাও যে, x=12(3+5cosθ) ও y=12(−4+5sinθ) দ্বারা মূলবিন্দুগামী একটি বৃত্ত সূচিত হয়। বৃত্তটির কেন্দ্রের স্থানাঙ্ক ও ব্যাসার্ধ নির্ণয় করো।
05:39View SolutionThe ends of a quadrant of a circle have the coordinates (1, 3) and (3, 1). Then the center of such a circle is
02:11View SolutionThe equation of the circle which touches the axes of coordinates and the line x3+y4=1 and whose center lies in the first quadrant is x2+y2−2cx−2cy+c2=0 , where c is (a) 1 (b) 2 (c) 3 (d) 6
07:44View SolutionThe equation of the circle which touches the axes of coordinates and the line x3+y4=1 and whose center lies in the first quadrant is x2+y2−2cx−2cy+c2=0 , where c is (a) 1 (b) 2 (c) 3 (d) 6
07:15View Solutionयदि एक वृत्त के केन्द्र एवं वृत्त पर एक बिन्दु के निर्देशांक क्रमशः C(3, -4) एवं A(-2, 1) हैं, तो वृत्त की त्रिज्या "r" =
03:51View SolutionOne end of the diameter of a circle is (1, 4). The center of the circle is '(3,-4)'.
Find the coordinates of the other end.03:09View Solution

