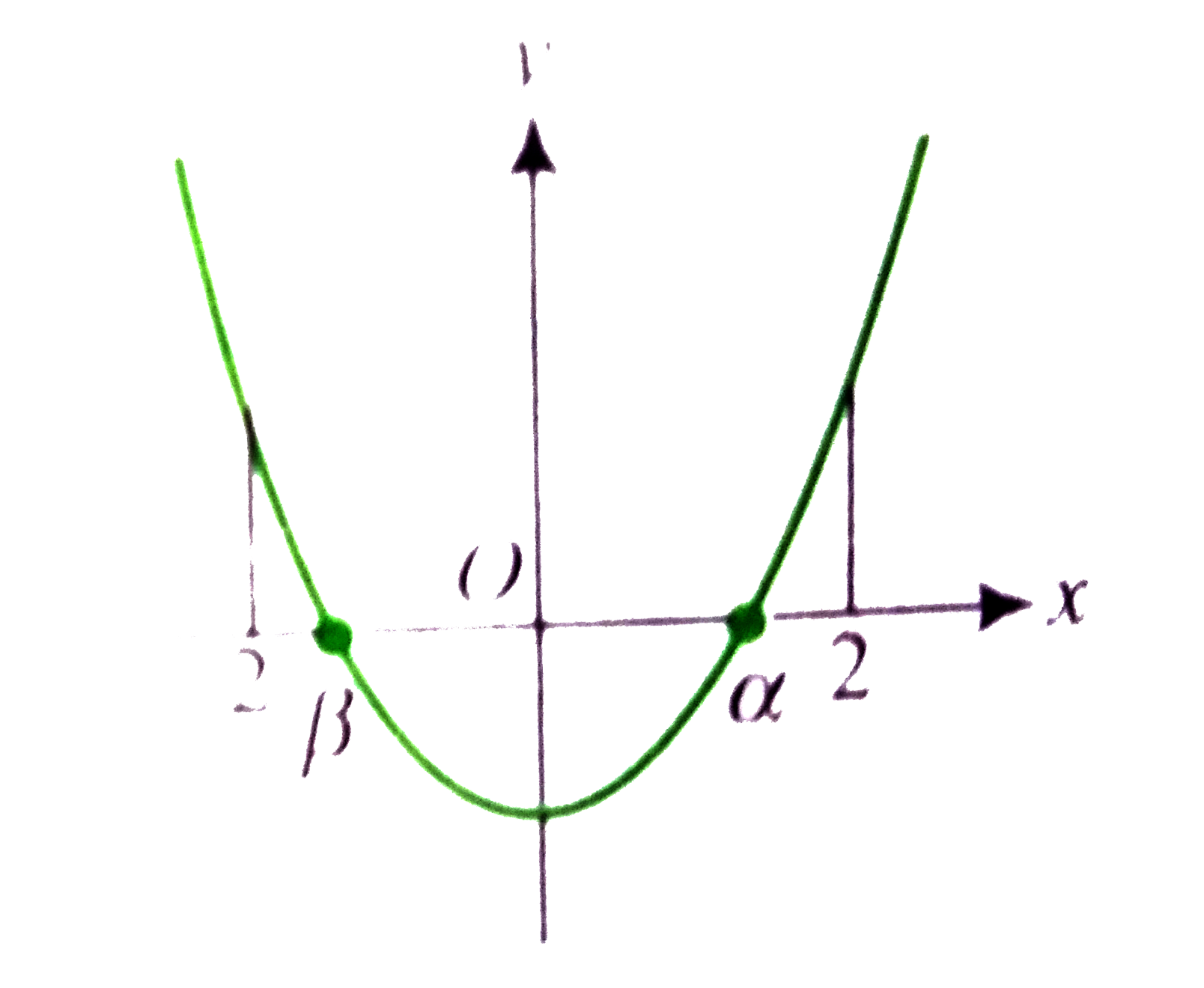
Consider a quadratic equation ax^2 + bx + c = 0 having roots alpha, b

Let a, b, c $\in$ R and $α, β$ are the real roots of the equation ax2 + bx + c = 0 and if a + b + c < 0, a – b + c < 0 and c > 0 then $[α] + [β]$ is equal to (where [.] denotes the greatest integer function.)
A0
B1
C $- 1$
DNone
If the roots of a quadratic equation $a x^{2} + b x + c = 0$ are $α and β$ then the quadratic equation having roots $α^{2} and β^{2}$ is :
A $x^{2} - (b^{2} - 2 a c) x + c = 0$
B $a^{2} x^{2} - (b^{2} - 2 a c) x + c = 0$
C $a x^{2} - (b^{2} - 2 a c) x + c^{2} = 0$
D $a^{2} x^{2} - (b^{2} - 2 a c) x + c^{2} = 0$

Consider a quadratic equation $a x^{2} + b x + c = 0$ having roots $α, β$ . If $4 a + 2 b + c > 0, a - b + c < 0 and 4 a - 2 b + C > 0$ then $| [α] + [β] |$ can be {where [] is greatest integer}