If the inequality cot2x+(k+1)cotx−(k−3)<0 is true for at least one x∈(0,π/2), then k∈.

A

(−∞,3−2√5)

B

(3,∞)

C

(−1,∞)

D

(−∞,3)

Text Solution
Verified by Experts

The correct Answer is:1,2

Let cot x = t.
Since x∈(0,π/2),t∈(0,∞)
Therefore, f(t)=t2+(k+1)t−(k−3)<0 for at least one t∈(0,∞) .
We have following possibilities for the graph of f(t).
Case I :
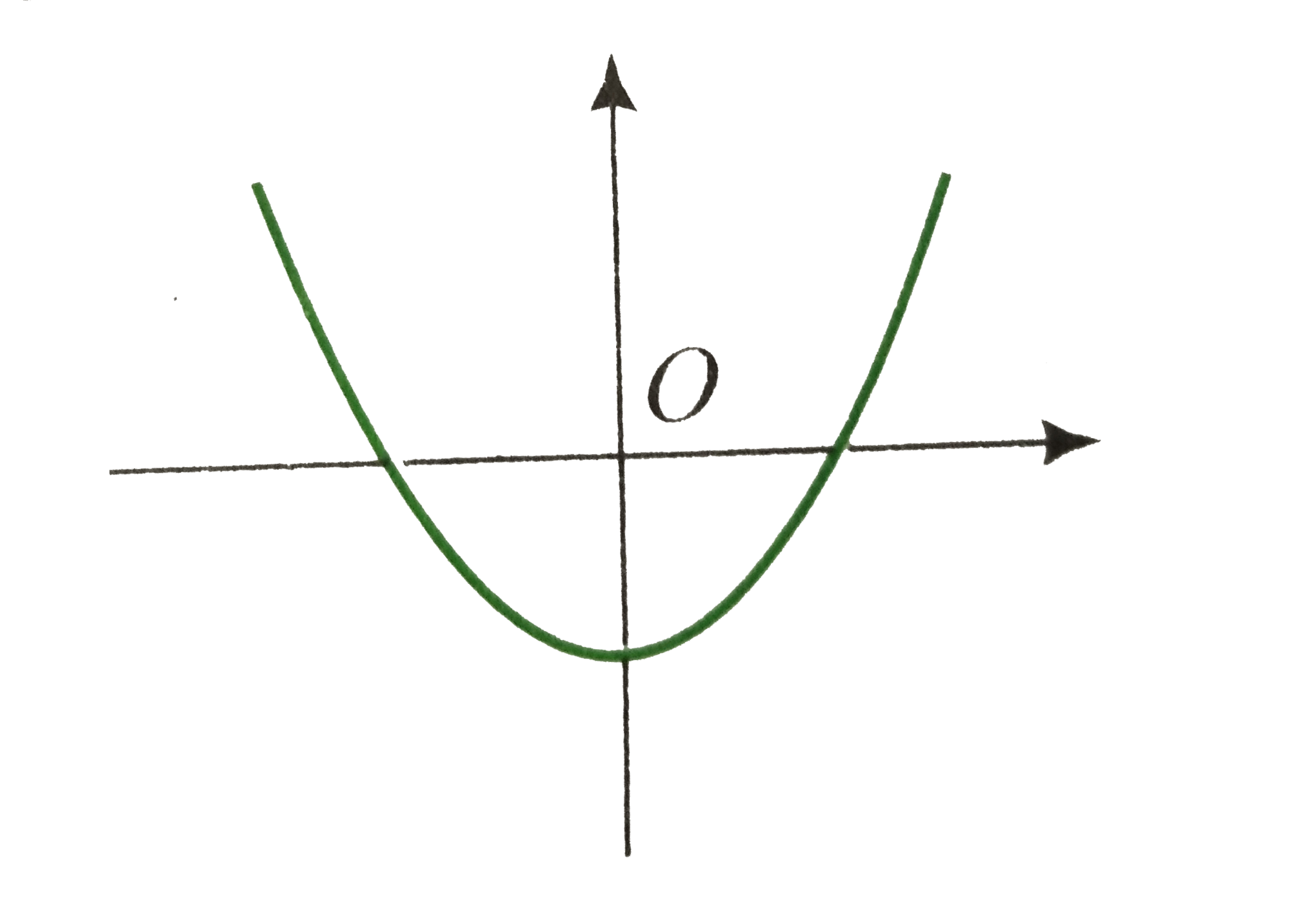
ocr_image
f(0)<0⇒k>3
Case II :
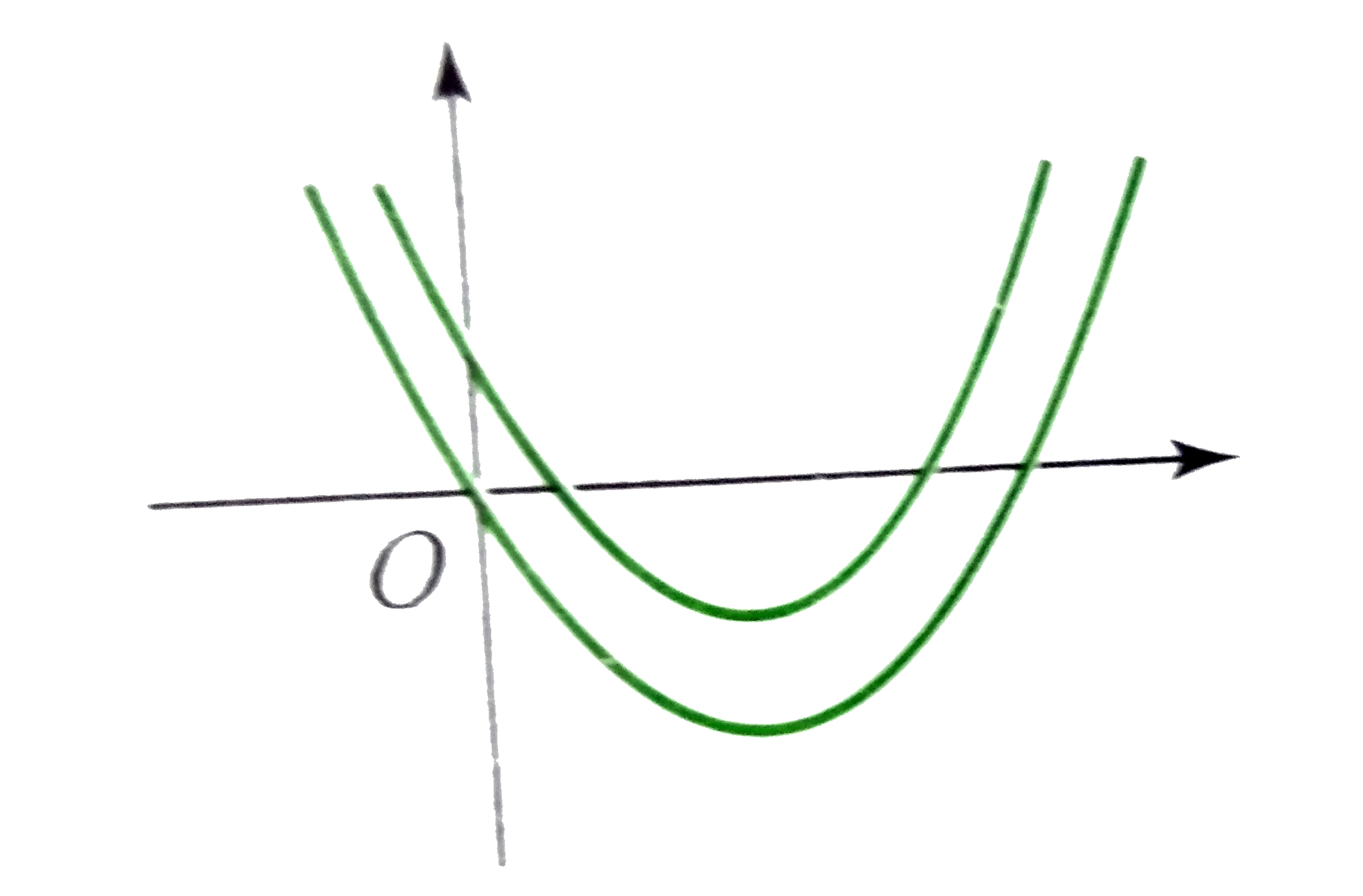
ocr_image
D>0
⇒(k+1)2+4(k−3)>0
⇒k2+6k−11>0
⇒(k+3)2>20
⇒k+3<−2√5ork+3>2√5
⇒k<−3−2−√2ork>−3+2√5
−b2a>0
⇒−(k+1)>0
⇒k<−1.....(2)
⇒k(0)≥0
⇒−k+3≥0
⇒k≤3....(3)
From (1),(2) and (3) we get
k∈(−∞,−3−2√5)
So, from the both cases, k∈(−∞,−3−2√5)∪(3,∞)

Doubtnut Promotions Banner
|
Class 12MATHSQUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Solution set of the inequality
    (cot−1x)2−(5cot−1x)+6>0 is

    A(cot3,cot2)
    B(−∞,cot2)∪(cot2,∞)
    C(cot2,∞)
    DNone of the above

  • All x satisfying the inequality (cot−1x)2−7(cot−1x)+10>0 lie in the interval,

    A(−∞,cot5)∪(cot4,cot2)
    B(cot5,cot4)
    C(cot2,∞)
    D(−∞,cot5)∪(cot2,∞)

  • The solution set of inequality (cot−1x)(tan−1x)+(2−π2)cot−1x−3tan−1x−3(2−π2)>0, is

    Ax∈(tan2,tan3)
    Bx∈(cot3,cot2)
    Cx∈(−∞,tan2)∪(tan3,∞)
    Dx∈(−∞,cot3)∪(cot2,∞)