Question

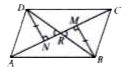
ABCD is a quadrilateral. AM and CN are perpendiculars to BD, AM= CN and diagonals AC and BD intersect at O, then which one of the following is correct?

Options

A. AO=OC
B. BO=OD
C. AO=BO
D. CO=DO

Answer

A

Explanation

To solve the problem, we need to analyze the given quadrilateral ABCD and the conditions provided. Here’s a step-by-step solution:

Step 1: Understand the Given Information
We have a quadrilateral ABCD. Points M and N are the feet of the perpendiculars dropped from points A and C to the line BD, respectively. It is given that AM = CN and that the diagonals AC and BD intersect at point O.

Step 2: Identify the Triangles
We will focus on the triangles AMO and CNO. These triangles are formed by the points A, M, O and C, N, O respectively.

Step 3: Analyze the Triangles
1. Perpendiculars: Since AM and CN are both perpendicular to BD, we have:
- Angle AMO = 90°
- Angle CNO = 90°

2. Given Lengths: We know that AM = CN (given).

3. Vertically Opposite Angles: The angles AOM and CON are vertically opposite angles, which means:
- Angle AOM = Angle CON

Step 4: Apply the Criteria for Congruence
Now we can use the Angle-Angle-Side (AAS) criterion for triangle congruence:
- Triangle AMO and triangle CNO have:
- AM = CN (given)
- Angle AMO = Angle CNO = 90° (both are right angles)
- Angle AOM = Angle CON (vertically opposite angles)

Since we have two angles and the side between them equal, we can conclude that:
- Triangle AMO ≅ Triangle CNO (by AAS criterion).

Step 5: Conclusion
From the congruence of triangles AMO and CNO, we can deduce that:
- AO = OC (by Corresponding Parts of Congruent Triangles - CPCT).

Thus, the correct option is that AO = OC.