Squares ABDE and ACFH are drawn externally on the sides AB and AC respectively of a scalene ΔABC. Which one of the following is correct?
BH=CE
AD = AF
BF=CD
DF = EH
The correct Answer is:A
To solve the problem, we need to analyze the given information about the scalene triangle ABC and the squares ABDE and ACFH constructed on its sides AB and AC respectively. We will follow a systematic approach to derive the necessary relationships and congruencies.
1. Draw the Triangle and Squares:
- Begin by sketching triangle ABC, ensuring it is scalene (all sides of different lengths).
- Draw square ABDE on side AB and square ACFH on side AC.
2. Label the Points:
- Label the vertices of triangle ABC as A, B, and C.
- For square ABDE, label the vertices as follows: A at the top left, B at the bottom left, D at the bottom right, and E at the top right.
- For square ACFH, label the vertices as follows: A at the top left, C at the bottom left, F at the bottom right, and H at the top right.
3. Identify Angles:
- Note that in square ABDE, angle BAE is 90 degrees, and in square ACFH, angle CAH is also 90 degrees.
- Therefore, we can write the following relationships:
- Angle BAE + Angle BAC + Angle CAE = 90° + Angle BAC + Angle CAE = 90° + Angle BAC + Angle CAH.
4. Establish Relationships Between Angles:
- From the previous step, we can conclude:
- Angle CAE = Angle BAH (since both angles are equal to the angle BAC).
5. Consider Triangles EAC and HAB:
- Now, we will analyze triangles EAC and HAB.
- In triangle EAC:
- EA = AB (sides of square ABDE)
- AC = AH (sides of square ACFH)
- Angle CAE = Angle BAH (as established earlier).
6. Apply the SAS Congruence Criterion:
- Since we have two sides and the included angle equal in both triangles:
- Triangle EAC is congruent to triangle HAB by the Side-Angle-Side (SAS) criterion.
7. Conclude with Corresponding Parts:
- By the Corresponding Parts of Congruent Triangles (CPCT), we can conclude:
- EC = BH.
Final Result:
Thus, we have established that the segments EC and BH are equal, which is a significant relationship derived from the properties of the squares and the triangle.
- Begin by sketching triangle ABC, ensuring it is scalene (all sides of different lengths).
- Draw square ABDE on side AB and square ACFH on side AC.
- Label the vertices of triangle ABC as A, B, and C.
- For square ABDE, label the vertices as follows: A at the top left, B at the bottom left, D at the bottom right, and E at the top right.
- For square ACFH, label the vertices as follows: A at the top left, C at the bottom left, F at the bottom right, and H at the top right.
- Note that in square ABDE, angle BAE is 90 degrees, and in square ACFH, angle CAH is also 90 degrees.
- Therefore, we can write the following relationships:
- Angle BAE + Angle BAC + Angle CAE = 90° + Angle BAC + Angle CAE = 90° + Angle BAC + Angle CAH.
- From the previous step, we can conclude:
- Angle CAE = Angle BAH (since both angles are equal to the angle BAC).
- Now, we will analyze triangles EAC and HAB.
- In triangle EAC:
- EA = AB (sides of square ABDE)
- AC = AH (sides of square ACFH)
- Angle CAE = Angle BAH (as established earlier).
- Since we have two sides and the included angle equal in both triangles:
- Triangle EAC is congruent to triangle HAB by the Side-Angle-Side (SAS) criterion.
- By the Corresponding Parts of Congruent Triangles (CPCT), we can conclude:
- EC = BH.
Thus, we have established that the segments EC and BH are equal, which is a significant relationship derived from the properties of the squares and the triangle.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Self Assessment Sheet10videos
TRIANGLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Self Assessment Sheet10videos
TRIANGLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TIME AND WORK EXERCISE - Self Assessment Sheet - 2010videos
TIME AND WORK
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - Self Assessment Sheet - 401videos
TRIGONOMETRICAL RATIOS
Similar Questions
Equilateral triangles ABD and ACE are drawn on sides AB and AC respectively of a ΔABC outside it. Prove that :
(i) ∠DAC=∠EAB (ii) DC=BEView SolutionIn ΔABC, C is right angle and a perpendicular 'p' is drawn on side AB. If a, b, c are length of sides BC, CA, AB respectively then which of the following is correct?
View Solution
Knowledge Check
- Question 1 - Select One
From a point O in the interior of a DeltaABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
AAF2+BD2+CE2=AE2+CD2+BF2BAB2+BC2=AC2CAF2+BD2+CE2=OA2+OB2+OC2DAF2+BD2+CE2=OD2+OE2+OF2 - Question 2 - Select One
D, E and Fare respectively the midpoints of the sides of ΔABC. Which of the following is true?
 AArea of ΔDEF= Area of ΔABCBArea of ΔDEF=12 Area of ΔABCCArea of ΔDEF= 13Area of ΔABCDArea of ΔDEF=14 Area of ΔABC
AArea of ΔDEF= Area of ΔABCBArea of ΔDEF=12 Area of ΔABCCArea of ΔDEF= 13Area of ΔABCDArea of ΔDEF=14 Area of ΔABC - Question 3 - Select One
X and Y are points on sides AB and AC respectively of ΔABC. For which of the following cases will XY be parallel to BC?
AAX = 1.3 cm, XB = 3.9 cm,
AY = 2.8 cm, YC = 5.6 cm,BAX = 1.3 cm, XB = 3.9 cm,
AY = 2.8 cm, YC = 8.4 cmCAX = 1.3 cm, XB = 2.6 cm,
AY = 2.8 cm, YC = 8.4 cmDAX = 1.3 cm, XB = 2.6 cm,
AY = 2.8 cm, YC = 11.2 cm
The given figure showns a parallelogram ABCD. Squares ABPQ and ADRS are drawn on sides AB and AD respectively of the parallelogram ABCD. Prove that :
(i) ∠SAQ=∠ABC
(ii) SQ=AC
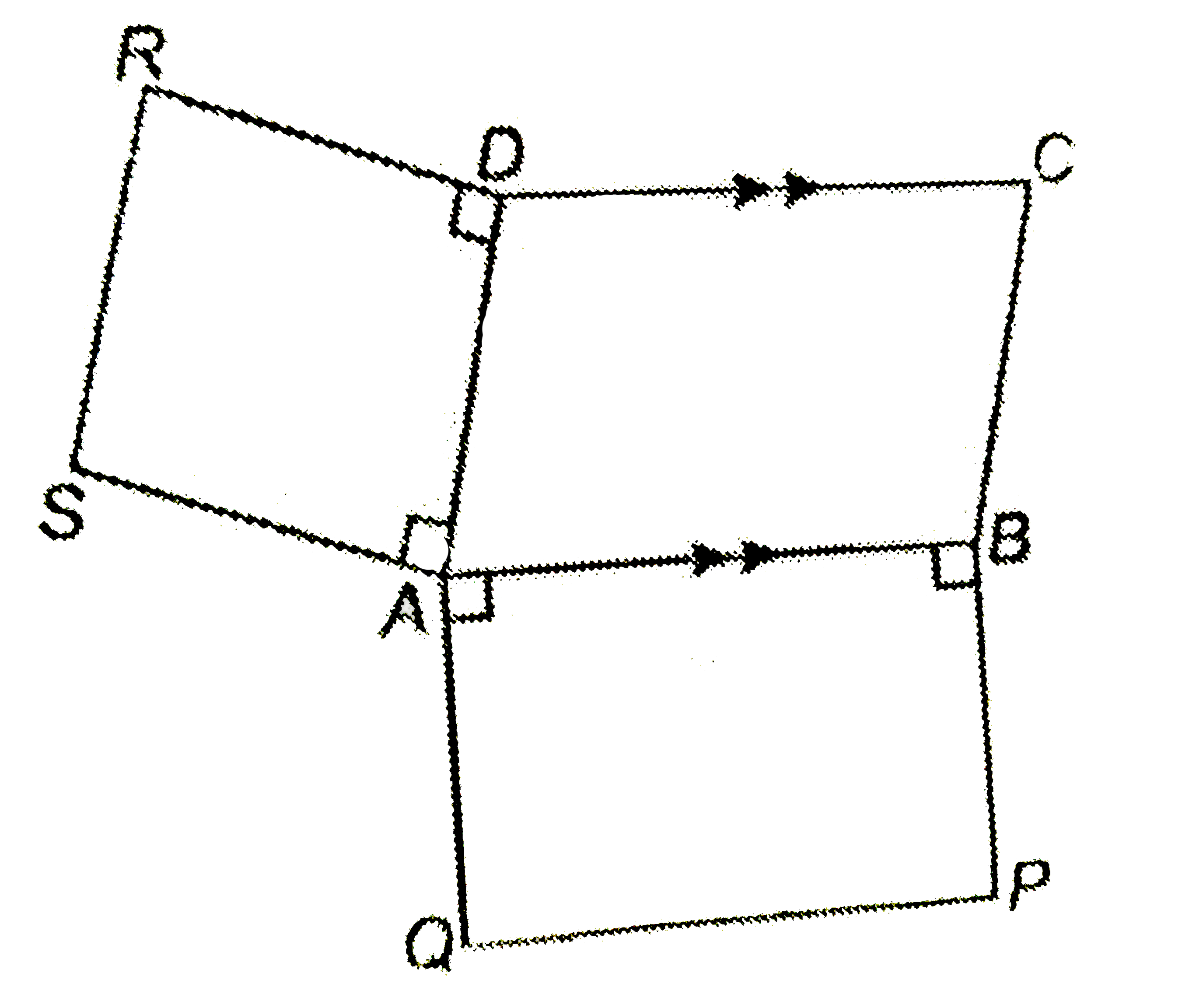 View Solution
View SolutionFrom a point O in the interior of a ΔABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
View SolutionIf AB, BC and AC be the three sides of a triangle ABC, then which one of the following is true?
View SolutionIn a triangle ABC, if AB,BC and AC are the three sides of the triangle, then which of the statements is necessarily?
View SolutionIn the given figure, the two sides AB and BC, and the median AD of ΔABC are correspondingly equal to the two sides PQ and QR, and the medium PM of ΔPQR. Prove that ΔABC≅ΔPQR.
View Solution

