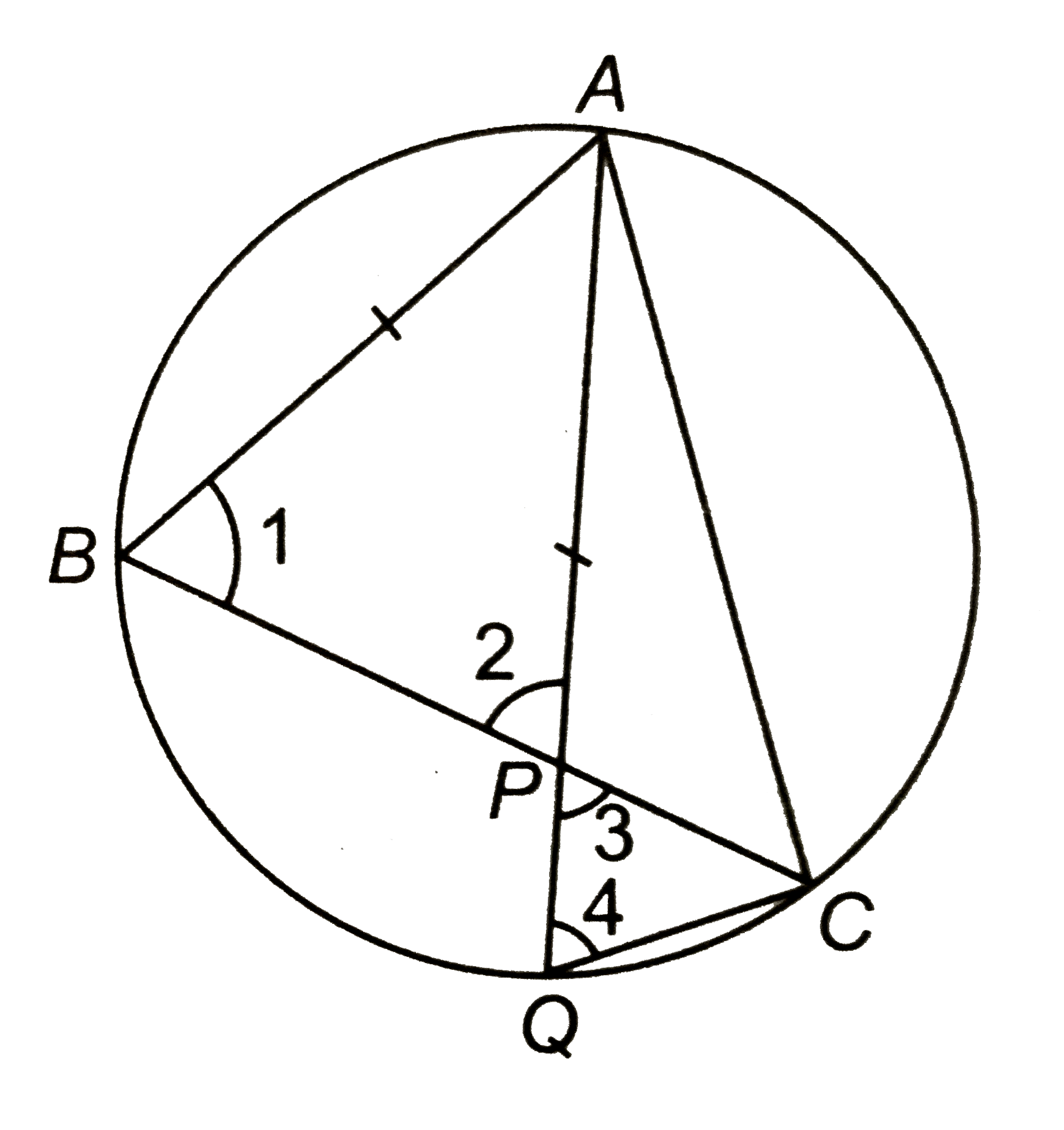
ΔABC is a triangle with the point P on side BC such that 3BP=2PC, the point Q is on the line CA such that 4CQ=QA. Find the ratio in which the line joining the common point R of AP and BQ and the point S divides AB.Solution in Punjabi
The correct Answer is:6:1
let S be the point of intersection of AB and CR. Let A be the origin and the position vectors of the points, B,C,P,Q,R and S be b,c,p,q,r and s respectively.
∴p=3b+2c5
and q=4c5 . .. (i)
⇒5q−3b2=5q4⇒10p−6b=5q
i.e., 10p=5q+6b⇒10p11=5q+6b11=r

⇒11r10=r=3b+2c5 [using Eq. (ii)]
11r=6b+4c ltbgt 11r−4c=6b
11r−4c7=67b=s, thus s divides AB in the ratio 6:1.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)9videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Single Integer Answer Type Questions)7videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
If vectors −−→AB=−3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are the sides of a ΔABC, then the length of the median throught A is
04:02View SolutionIf the resultant of three forces F1=pˆi+3ˆj−ˆk,F2=6ˆi−ˆkandF3=−5ˆi+ˆj+2ˆk acting on a particle has a magnitude equal to 5 units, then the value of p is
00:58View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
02:58View SolutionP,Q,R are the points of intersection of a line t with sides BC,CA,AB of a Delta ABC respectively,then (BP)/(PC)*(CO)/(QA)*(AR)/(RB)=
02:25View SolutionΔABC एक समबाहु त्रिभुजा हे, बिंदु P,Q,R भुजा AB,BC,CA के बिंदु हे, तब
02:46View Solutionदी आकृति में, ABC एक त्रिभुज है तथा भुजा BC पर एक बिन्दु P इस प्रकार है की AB = AP है | यदि बढ़ाई गई AP, ΔABC के परिवृत्त को Q पर मिलती है तो सिद्ध कीजिए कि CP = CQ.
 10:36View Solution
10:36View SolutionFind the ratio in which point T(−1,6) divides the line segment joining the points P(−3,10)andQ(6,−8)
09:30View SolutionThe ratio in which he line-segment joining the points (p,q,r)and(−p,−r,−q) is divided by the zx-plane, is-
06:16View SolutionIn △ABC, if the points P, Q, R divides the sides BC, CA, AB in the ratio 1:4, 3:2, 3:7 respectively and the point S divides side AB in the ratio 1:3, then (¯¯¯¯¯¯AP+¯¯¯¯¯¯BQ+¯¯¯¯¯¯CR):(¯¯¯¯¯CS)=
View SolutionIn ΔABC, P is the mid point of BC,Q divides CA internally in the ratio 2:1 and R divides AB externally in the ratio 1:2 then
04:01View SolutionIn Δ ABC, P, Q, R are points on BC, CA and AB respectively, dividing them in the ratio 1 : 4, 3 : 2 and 3 : 7. The point S divides AB in the ratio 1 : 3. Then |AP+BQ+CR|∣∣→CS∣∣=
02:00View SolutionIf P, Q, R are the mid-point of the sides AB, BC and CA of ΔABC respectively, then PC−BQ=
05:16View SolutionThe ratio in which the point Q(5,4,−6) divides the line joining the points P(3,2,−4) and R(9,8,−10) is
05:20View SolutionThe triangle is formed by joining the mid point of the sides AB, BC and CA of ΔABC and the area of ΔPQR is 6cm2, then the area of ΔABC is :
02:58View SolutionIn ΔABC, P is a point on the side BC such that 3BP = 2PC. Q is a point on the side CA such that 4CQ = QA. The lines AP and BQ intersect in R. Produce the line CR to meet the side AB in S. Find the ratio in which S divides AB.
06:03View SolutionIn DeltaABC , P is the mid point of BC,Q divides CA internally in the ratio 2:1 and R divides AB externally in the ratio 1:2 then
01:03View Solution

