Let [x] be the greatest integer function f(x)=⎛⎜
⎜⎝sin(14(π[x]))[x]⎞⎟
⎟⎠ is
(a)Not continuous at any point
(b)continuous at x=32
(c)discontinuous at x = 2
(d)differentiable at x=43 Solution in Punjabi
(a)Not continuous at any point
(b)continuous at x=32
(c)discontinuous at x = 2
(d)differentiable at x=43
The correct Answer is:B, C, D
Step by step video & image solution for Let [x] be the greatest integer function f(x)=(sin(1/4(pi[x]))/([x])) is (a)Not continuous at any point (b)continuous at x = (3)/(2) (c)discontinuous at x = 2 (d)differentiable at x = (4)/(3) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Statement I And Ii Type Questions)
11 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 4
3 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Single Option Correct Type Questions)
50 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
3 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
Similar Questions
Statement I f(x)=sinx+[x] is discontinuous at x = 0.
Statement II If g(x) is continuous and f(x) is discontinuous, then g(x) + f(x) will necessarily be discontinuous at x = a.
View SolutionA man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
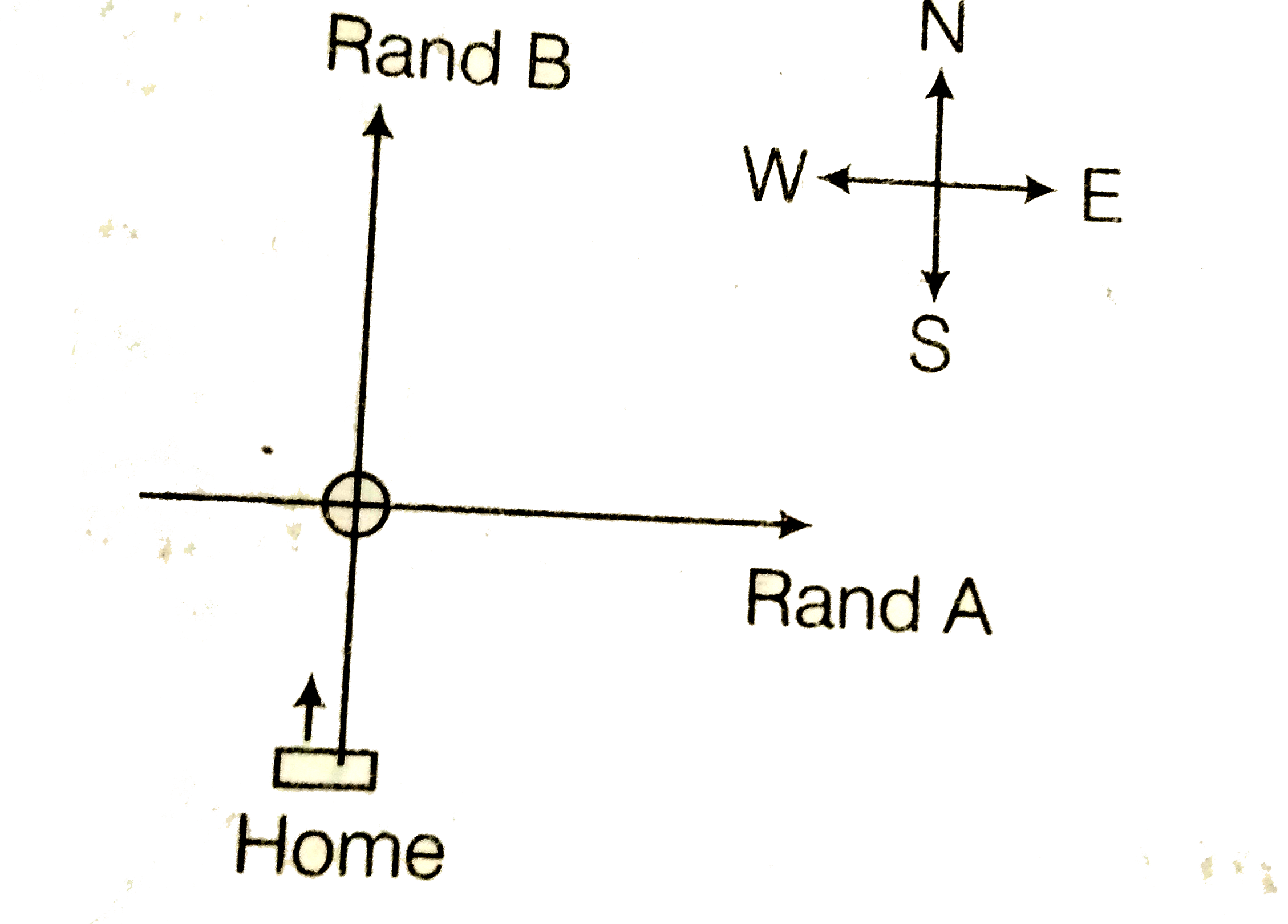
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Now if roads A and B are taken as X-axis and y-axis ,then visible point representing the graph of y=f(x)
Then the value of x at which function f(x) is discontinous
View SolutionIf f(x)={sinπx2,x<1[x],x≥1, where [x] denotes the greatest integer function, then
View SolutionFind the modules of 2+3ι
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View SolutionIf g(x)=2h(x)+|h(x)|2h(x)−|h(x)| where h(x)=sinx−sinnx,n∈R+, the set of positive real numbers, and f(x)={[g(x)],x(0,π2)∪(π2,π)and3,x=π2 where [.] denotes greatest integer function. Then (a)f(x) is continuous and differentiable at x=π2, when 0<n<1 (b)f(x) is continuous and differentiable at x=π2, when n>1 (c)f(x) is discontinuous and non differentiable at x=π2,for0<n<1 (d)f(x) is continuous but not differentiable at x=π2, when n>1
View SolutionThe number of points where f(x)=[sin x+cos x] (where [.] denotes the greatest integer function x in(0,2 pi) is not continuous is (A) 3(B)4(C)5(D)6
View Solutionf(x)={(x[x],if 0 le x< 3),((x-1)[x],if 3lexle4)) where [x] is the greatest integer function. The function f(x) is (A) continuous and differentiable at x=3 (B) continuous at x=1,2,3 (C) continuous but not differentiable at x=3 (D) discontinuous at x=1,2,3
View SolutionThe function f(x)=(sin(π[x−π])) , where [] denotes the greatest integer function, is continuous as well as differentiable for all x∈R (b) continuous for all x but not differentiable at some x (c) differentiable for all x but not continuous at some x . (d) none of these
View SolutionFind the points of continuity or discontinuity and differentiability or non- differentiability of...f(x)=|[x]x| in 1<=x<=4, where [] denotes greatest integer function.
View SolutionLet f(x)=⎧⎪⎨⎪⎩1+xif x<01+[x]+sinx0≤x<π/23x≥π/2
Statement-1: F is a continuous on R-[1]
Statement-2: The greatest integer function is discontinuous at every integer point.
View Solution[" The function "f(x)={[(e^((x))-e^(x))/(e^(x)),,x<0],[(sin{x})/({tan x}),,,x>0," where "[.]" and "{.}" represent greatest integer and "],[2,,x=0]],[" fractional part functions respectively,is "],[[" (A) "," continuous at "x=0],[" (B) "," discontinuous at "x=0],[" (C) "," continuous at "x=(pi)/(6)],[" (D) "," discontinuous at "x=(pi)/(4)]]
View SolutionThe function f(x)=[√x1+x] ; (where [ ] denotes the greatest integer function) is
(A) Continuous but non-differentiable for x>0
(B) Continuous and differentiable for x≥0
(C) Discontinuous exactly at two points for x≥0
(D) Non-differentiable exactly at one point for x>0
View SolutionDiscuss continuity of f(x)=[sinx]−[cosx] at x=π/2, where [.] represent the greatest integer function .
View SolutionThe function f(x)=sin(π[x−π])4+[x]2 , where [] denotes the greatest integer function, (a) is continuous as well as differentiable for all x∈R (b) continuous for all x but not differentiable at some x (c) differentiable for all x but not continuous at some x . (d) none of these
View SolutionThe function f(x)=x−[x] , where [⋅] denotes the greatest integer function is (a) continuous everywhere (b) continuous at integer points only (c) continuous at non-integer points only (d) differentiable everywhere
View Solution
