The function f(x)=x−[x]
, where [⋅]
denotes the greatest
integer function is
(a) continuous
everywhere
(b) continuous at integer
points only
(c) continuous at non-integer
points only
(d) differentiable
everywhereSolution in Punjabi
is continuous for all positive integers
is discontinuous for all non-positive integers
has finite number of elements in its range
is such that its graph does not lie above the X-axis
The correct Answer is:A, B, C, D
Step by step video & image solution for The function f(x)=x-[x] , where [⋅] denotes the greatest integer function is (a) continuous everywhere (b) continuous at integer points only (c) continuous at non-integer points only (d) differentiable everywhere by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Statement I And Ii Type Questions)
11 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 4
3 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Single Option Correct Type Questions)
50 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
3 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
Similar Questions
Statement I f(x)=sinx+[x] is discontinuous at x = 0.
Statement II If g(x) is continuous and f(x) is discontinuous, then g(x) + f(x) will necessarily be discontinuous at x = a.
View SolutionA man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
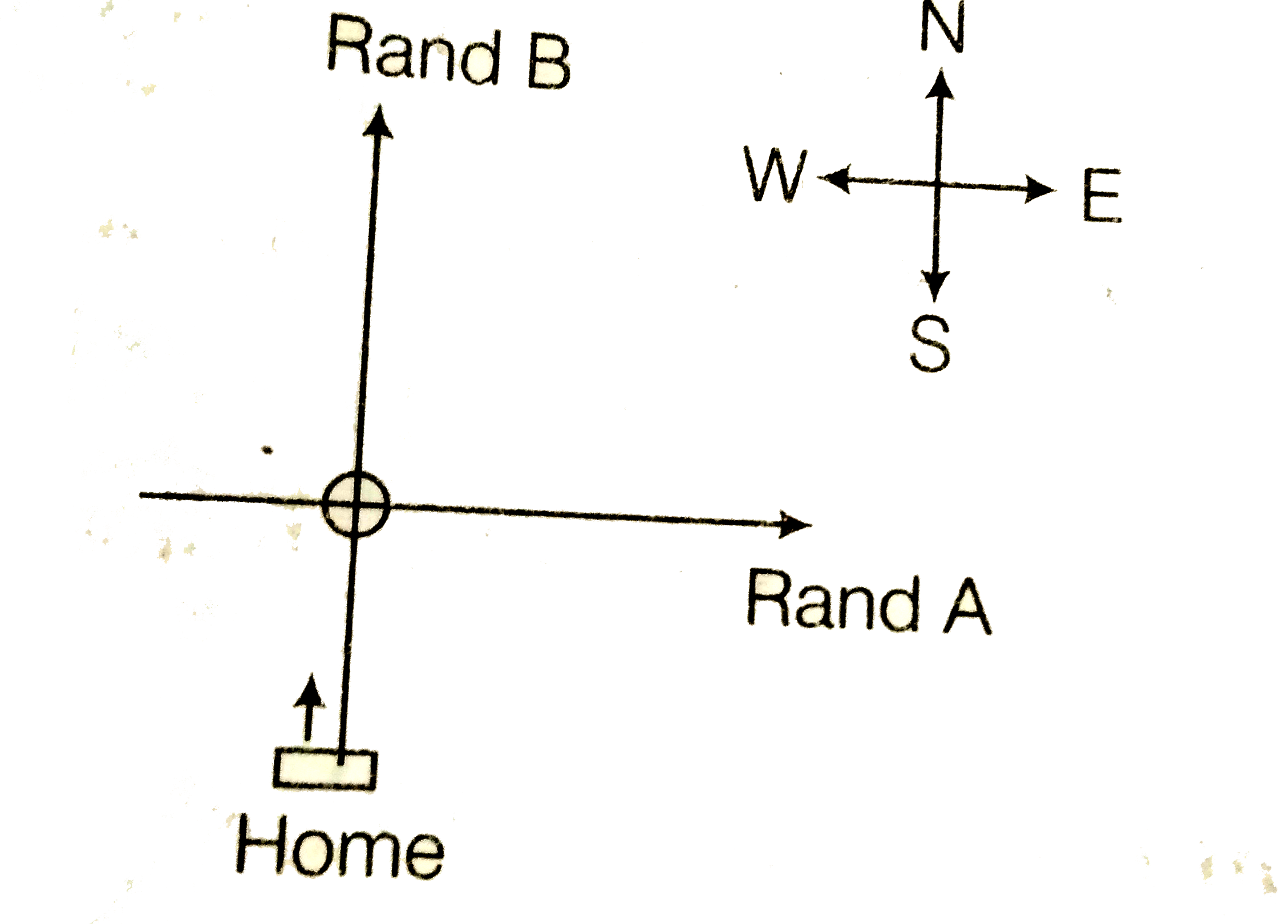
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Now if roads A and B are taken as X-axis and y-axis ,then visible point representing the graph of y=f(x)
Then the value of x at which function f(x) is discontinous
View SolutionIf f(x)={sinπx2,x<1[x],x≥1, where [x] denotes the greatest integer function, then
View SolutionFind the modules of 2+3ι
View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
View SolutionThe function f(x)=e−|x| is continuous everywhere but not differentiable at x=0 continuous and differentiable everywhere not continuous at x=0 none of these
View SolutionThe function f(x)=x−[x] , where [] denotes the greatest integer function is (a) continuous everywhere (b) continuous at integer points only (c) continuous at non-integer points only (d) differentiable everywhere
View SolutionThe function f(x)=e^(|x|) is (a) Continuous everywhere but not differentiable at x=0 (b) Continuous and differentiable everywhere (c) Not continuous at x=0 (d) None of the above
View SolutionFind the points of continuity or discontinuity and differentiability or non- differentiability of...f(x)=|[x]x| in 1<=x<=4, where [] denotes greatest integer function.
View SolutionThe number of points at which the function f(x)=(1)/(x-[x])([.] denotes,the greatest integer function) is not continuous is
View SolutionIf limx→af(x)=limx→a[f(x)]andf(x) is non-constant continuous function, where [.] denotes the greatest integer function, then
View SolutionThe function f(x)=[x], where [x] denotes the greatest integer function,is continuous at
View SolutionIs greatest integer function [x] is continuous everywhere ?
View SolutionThe function f(x)=[√x1+x] ; (where [ ] denotes the greatest integer function) is
(A) Continuous but non-differentiable for x>0
(B) Continuous and differentiable for x≥0
(C) Discontinuous exactly at two points for x≥0
(D) Non-differentiable exactly at one point for x>0
View SolutionA point where function f(x)=[sin[x]] is not continuous in (0,2π) [.] denotes the greatest integer ≤x, is
View SolutionThe function f(x)=e−|x| is continuous everywhere but not differentiable at x=0 continuous and differentiable everywhere not continuous at x=0 none of these
View Solution
