x51+16 is divided by (x +1), the remainder obtained is ?
1
2
0
15
The correct Answer is:d
To find the remainder when x51+16 is divided by x+1, we can use the Remainder Theorem. The Remainder Theorem states that the remainder of the division of a polynomial f(x) by x−c is equal to f(c).
1. Identify the polynomial and the divisor:
- The polynomial is f(x)=x51+16.
- The divisor is x+1, which can be rewritten as x−(−1). Thus, we will evaluate f(−1).
2. Substitute x=−1 into the polynomial:
- We need to calculate f(−1):
f(−1)=(−1)51+16
3. Evaluate (−1)51:
- Since 51 is an odd number, (−1)51=−1.
4. Calculate f(−1):
- Now substitute back into the equation:
f(−1)=−1+16
- Simplifying this gives:
f(−1)=15
5. Conclusion:
- Therefore, the remainder when x51+16 is divided by x+1 is 15.
Final Answer:
The remainder is 15.
- The polynomial is f(x)=x51+16.
- The divisor is x+1, which can be rewritten as x−(−1). Thus, we will evaluate f(−1).
- We need to calculate f(−1):
f(−1)=(−1)51+16
- Since 51 is an odd number, (−1)51=−1.
- Now substitute back into the equation:
f(−1)=−1+16
- Simplifying this gives:
f(−1)=15
- Therefore, the remainder when x51+16 is divided by x+1 is 15.
The remainder is 15.
Topper's Solved these Questions
Similar Questions
Knowledge Check
When
 is divided by 10, the remaindeer obtained is ? A3B1C2D9
is divided by 10, the remaindeer obtained is ? A3B1C2D9When
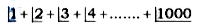 is divided by 12, the remainder obtained is? A6B5C9D7
is divided by 12, the remainder obtained is? A6B5C9D7If (x11+1) is divided by (x+1), then the remainder is :
A2B0C11D12
When x2−7x+15 is divided by (x - 3), the remainder obtained is ?
View SolutionWhen
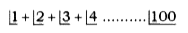 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?
View SolutionIf (2x3+5x2−4x−6) is divided by (2x+1), then the remainder obtained is ?
View Solution444444444 divided by 13, the remainder obtained is ?
View SolutionWhen x3+5x2+10k is divided by (x2+2) the remainder obtained is −2x, then the value of k is
View Solution

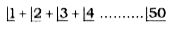 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?