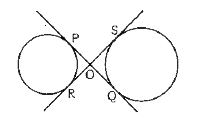
PQ and RS are common tangents of two circles intersection at A and B. AB, when produced both sides, meet the tangents PQ and RS at x and y, respectively. If AB = 3 cm, xy = 5 cm, then PQ (in cm) will be.
3 cm
4 cm
5 cm
2 cm
To find the length of PQ, we can use the relationship between the lengths of the segments formed by the tangents and the line segment connecting the points of intersection of the two circles. The formula we will use is:
PQ2=XY2−AB2
1. Identify the given lengths:
- Length of AB = 3 cm
- Length of XY = 5 cm
2. Square the lengths of XY and AB:
- XY2=52=25
- AB2=32=9
3. Substitute the squared values into the formula:
- Using the formula PQ2=XY2−AB2:
PQ2=25−9
4. Calculate PQ^2:
PQ2=16
5. Find PQ by taking the square root:
PQ=√16=4 cm
Thus, the length of PQ is 4 cm.
- Length of AB = 3 cm
- Length of XY = 5 cm
- XY2=52=25
- AB2=32=9
- Using the formula PQ2=XY2−AB2:
PQ2=25−9
PQ2=16
PQ=√16=4 cm
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two circles intersect at A and B. P is a point on produced BA. PT and PQ are tangents to the circles. The relation of PT and PQ is
APT = 2PQBPT<PQCPT>PQDPT=PQPerimeter of two similar triangles ΔABC and ΔPQR are 36 cm and 24 cm respectively and if PQ = 10. Find AB.
A15 cmB12 cmC14 cmD26 cmAC is transverse common tangent to two circles with centres P and Q and radii 6 cm and 3 cm at the point A and C respectively. If AC cuts PQ at the point B and AB= 8cm then the length of PQ is:
A13 cmB12 cmC10 cmD15 cm
A and B are the centers of two circles with radii 11 cm and 6 cm respectively. A common tangent touches these circles at P and Q respectively. If AB = 13 cm, then the length of PQ is:
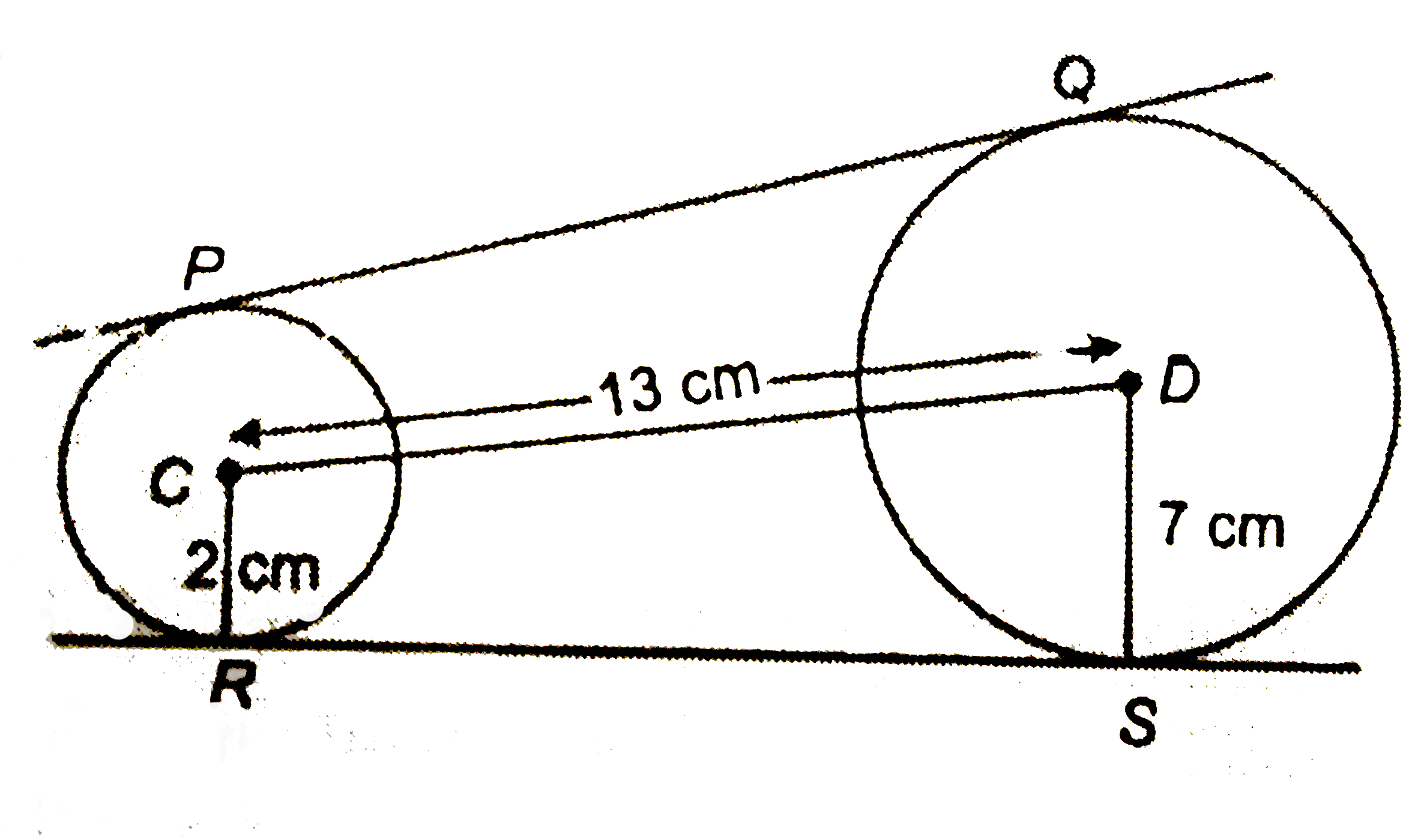
View SolutionIn the given diagram, PQ and RS are common tangents to the two circles with centres C and D. Find the length of PQ and hence area of trapexium RSDC.
View SolutionThe perimetes of two similar triangles ABC and PQR are 32 cm and 24 cm respectively. If PQ=12 cm, find AB.
View SolutionPQ and RS are two parallel tangents to a circle with centre O and another tangent AB wih point of contact C intersect PQ at A and RS at B. then find ∠AOB
View SolutionTwo circles Intersect at A and B. P is a point on produced BA. PT and PQ are tangents to the circles. The relation of PT and PQ is
View Solution