Two lines PQ and RS cut each other at X such that XP = XR. If ∠PSX=∠RQX then-
PR = QS
PS = RQ
∠XSQ=∠XRP
(ΔPXR)=(ΔQXS)
To solve the problem step by step, we will analyze the given information and apply the properties of triangles and congruence.
1. Understanding the Given Information:
We have two lines, PQ and RS, that intersect at point X. We are given that XP=XR and ∠PSX=∠RQX.
2. Drawing the Diagram:
Draw lines PQ and RS intersecting at point X. Mark the points P, Q, R, and S. Label the segments such that XP=XR.
3. Identifying Angles:
From the intersection, we can identify the angles:
- ∠PSX is formed by line PS and line PX.
- ∠RQX is formed by line RQ and line RX.
4. Using the Congruence Criteria:
We have two triangles:
- Triangle PXS
- Triangle RQX
We know:
- XP=XR (given)
- ∠PSX=∠RQX (given)
- By the property of vertical angles, ∠PXS=∠RQX (since they are vertical angles).
5. Applying the Side-Angle-Side (SAS) Congruence Theorem:
Since we have two sides and the included angle equal in both triangles:
- XP=XR
- ∠PSX=∠RQX
- ∠PXS=∠RQX
Therefore, by the SAS criterion, triangle PXS is congruent to triangle RQX.
6. Using Corresponding Parts of Congruent Triangles (CPCT):
From the congruence of triangles, we can conclude that:
- PS=RQ (corresponding sides of congruent triangles are equal).
7. Conclusion:
The correct answer is that PS=RQ.
We have two lines, PQ and RS, that intersect at point X. We are given that XP=XR and ∠PSX=∠RQX.
Draw lines PQ and RS intersecting at point X. Mark the points P, Q, R, and S. Label the segments such that XP=XR.
From the intersection, we can identify the angles:
- ∠PSX is formed by line PS and line PX.
- ∠RQX is formed by line RQ and line RX.
We have two triangles:
- Triangle PXS
- Triangle RQX
- XP=XR (given)
- ∠PSX=∠RQX (given)
- By the property of vertical angles, ∠PXS=∠RQX (since they are vertical angles).
Since we have two sides and the included angle equal in both triangles:
- XP=XR
- ∠PSX=∠RQX
- ∠PXS=∠RQX
From the congruence of triangles, we can conclude that:
- PS=RQ (corresponding sides of congruent triangles are equal).
The correct answer is that PS=RQ.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Two line segments PQ and RS intersect at X in such a way that XP=XR. If ∠PSX=∠RQX, then one must have
APR=QSBPS=RQC∠XSQ=∠XRPDar(ΔPXR)=ar(ΔQXS) - Question 2 - Select One
Two lines ¯¯¯AB and ¯¯¯CD cut each other at O .if ∠AOC=50∘ then ∠BOC is equal to
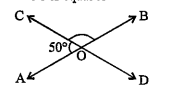 A40∘B50∘C140∘D130∘
A40∘B50∘C140∘D130∘ - Question 3 - Select One
Two lines ¯¯¯¯¯¯AB and ¯¯¯¯¯¯CD cut each other at O. If ∠AOC=50∘, than ∠BOC is equal to
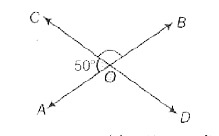 A40∘B50∘C140∘D130∘
A40∘B50∘C140∘D130∘
In Figure, two straight lines PQ and RS intersect each other at O. If ∠POT=750, find the values of a,b and c
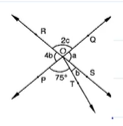 View Solution
View SolutionIn Fig. 12, two straight lines PQ and RS intersect each other at O. If ∠POT=750, find the values of a,b and ⋅
View SolutionLines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7, find all the angles.
View SolutionIn Fig: 6.9. lines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7,find the all the angles..
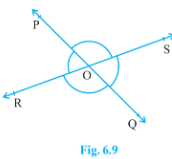 View Solution
View SolutionTwo circles of equal radii cut each other at P and Q, so that the centre of one lies on the other. A straight line through P cuts the circle again at A and B. Prove that ΔQAB is equilateral triangle.
View Solution

