The height AD of a triangle ABC is 20√2 cm. divides the triangle in two equal areas arts by a line which is parallel to the side BC. Find the distance from point A to L.
10 cm
10√2cm
15 cm
20 cm
To solve the problem, we need to find the distance from point A to point L in triangle ABC, where the height AD divides the triangle into two equal areas by a line parallel to side BC.
1. Understanding the Triangle and Given Information:
- We have triangle ABC with height AD = 20√2 cm.
- A line parallel to BC divides the triangle into two equal areas at point L.
2. Properties of Similar Triangles:
- Since the line through point L is parallel to side BC, triangles ABL and ABC are similar.
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
3. Setting Up the Area Ratio:
- Let the area of triangle ABC be A.
- Since the line divides the triangle into two equal areas, the area of triangle ABL is A2.
- The ratio of the areas of triangles ABL and ABC is 12.
4. Using the Area Ratio to Relate Heights:
- Let the height from point A to line L be AL.
- The ratio of the areas can be expressed in terms of the heights:
AreaABLAreaABC=(ALAD)2
- Substituting the known area ratio:
12=(AL20√2)2
5. Solving for AL:
- Taking the square root of both sides:
√12=AL20√2
- Simplifying √12=1√2:
1√2=AL20√2
- Cross-multiplying gives:
AL=20√2⋅1√2=20 cm
6. Conclusion:
- The distance from point A to point L is 20 cm.
Final Answer:
The distance from point A to point L is 20 cm.
- We have triangle ABC with height AD = 20√2 cm.
- A line parallel to BC divides the triangle into two equal areas at point L.
- Since the line through point L is parallel to side BC, triangles ABL and ABC are similar.
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
- Let the area of triangle ABC be A.
- Since the line divides the triangle into two equal areas, the area of triangle ABL is A2.
- The ratio of the areas of triangles ABL and ABC is 12.
- Let the height from point A to line L be AL.
- The ratio of the areas can be expressed in terms of the heights:
AreaABLAreaABC=(ALAD)2
- Substituting the known area ratio:
12=(AL20√2)2
- Taking the square root of both sides:
√12=AL20√2
- Simplifying √12=1√2:
1√2=AL20√2
- Cross-multiplying gives:
AL=20√2⋅1√2=20 cm
- The distance from point A to point L is 20 cm.
The distance from point A to point L is 20 cm.
Topper's Solved these Questions
Similar Questions
In Triangle ABC,BC=8,CA=6andAB=10. A line dividing the triangle ABC into regions of equal area is perpendicular to AB at point X. Find the value of BXI√2.
View SolutionIn triangle ABC,BC=8,CA=6,andAB=10,A line dividing the triangle ABC into two regions of equal area is perpendicular to AB at point X. Find the value of BX√2
View Solution
Knowledge Check
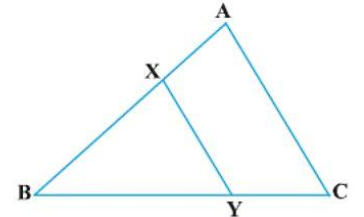
In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
A√2+1+√2B2−√2:2C1:√2D1:1
If ar(ΔABC) = 16 cm2 then find the area of the triangle formed by joining the mid points of the sides of ΔABC.
View SolutionEach side of triangle ABC is divided into three equal parts. Find the ratio of the are of hexagon PQRSTU to the area of the triangle ABC.
View SolutionProve that , "If a line parallel to a side of a triangle intersects the remaining sides in two distinct points then the line divides the sides in the same proportion".
View SolutionIn Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
View SolutionIn a triangle ABC, if AB = 20 cm, AC = 21 cm and BC = 29 cm, then find the distance vertex A and mid point of BC.
View SolutionThe area of a triangle ABC is 63 sq. units. Two parallel lines DE, FG, are drawn such that they divide the line segments AB and BC into three equal parts. What is the area of the quadrilateral DEGF ?
View SolutionIn triangle ABC , base BC and area of triangle are fixed. The locus of the centroid of triangle ABC is a straight line that is a) parallel to side BC (b)right bisector of side BC (c)perpendicular to BC (d)inclined at an angle sin−1(√BC) to side BC
View Solution
