In the diagram two circle (C-I, A) and (C-II, B) and ABR is a straight line which intersect with common tangent PQR of both circle at point R here AB = 25, PQ = 24, PA = 12
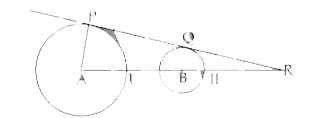
Ratio of AB and bR is
7:5
7:6
7:10
None of these
Step by step video & image solution for In the diagram two circle (C-I, A) and (C-II, B) and ABR is a straight line which intersect with common tangent PQR of both circle at point R here AB = 25, PQ = 24, PA = 12 Ratio of AB and bR is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.

View Solution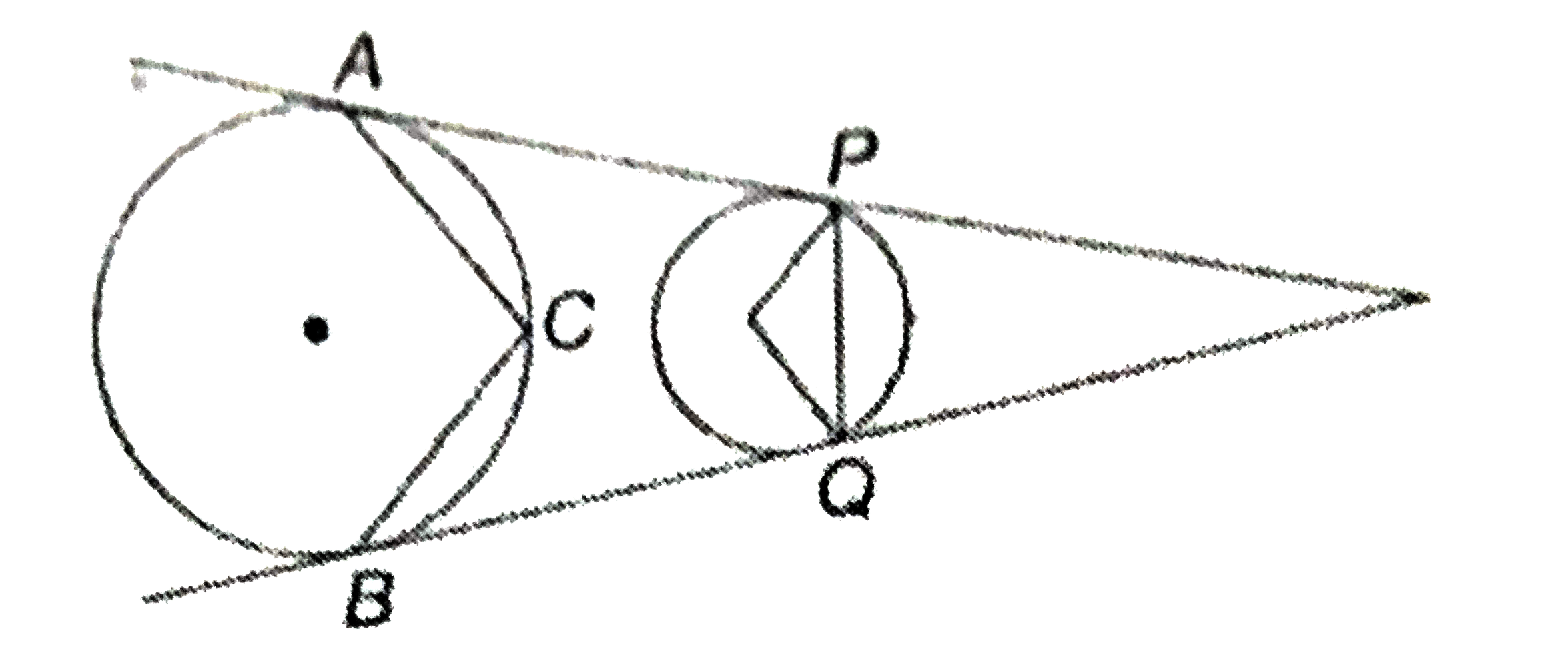
In the diagram above, A,B,P and Q are points of contacts of direct common tangents of the two circles. If ∠ACB is 120∘ , then find the angle between the two tangents and angle made by PQ at the centre of same circle.
View Solution
Knowledge Check
Suppose S1 and S2 are two unequal circles, AB and CD are the direct common tangents to these circles. A transverse common tangent PQ cuts AB in R and CD in S. If AB = 10, then RS is -
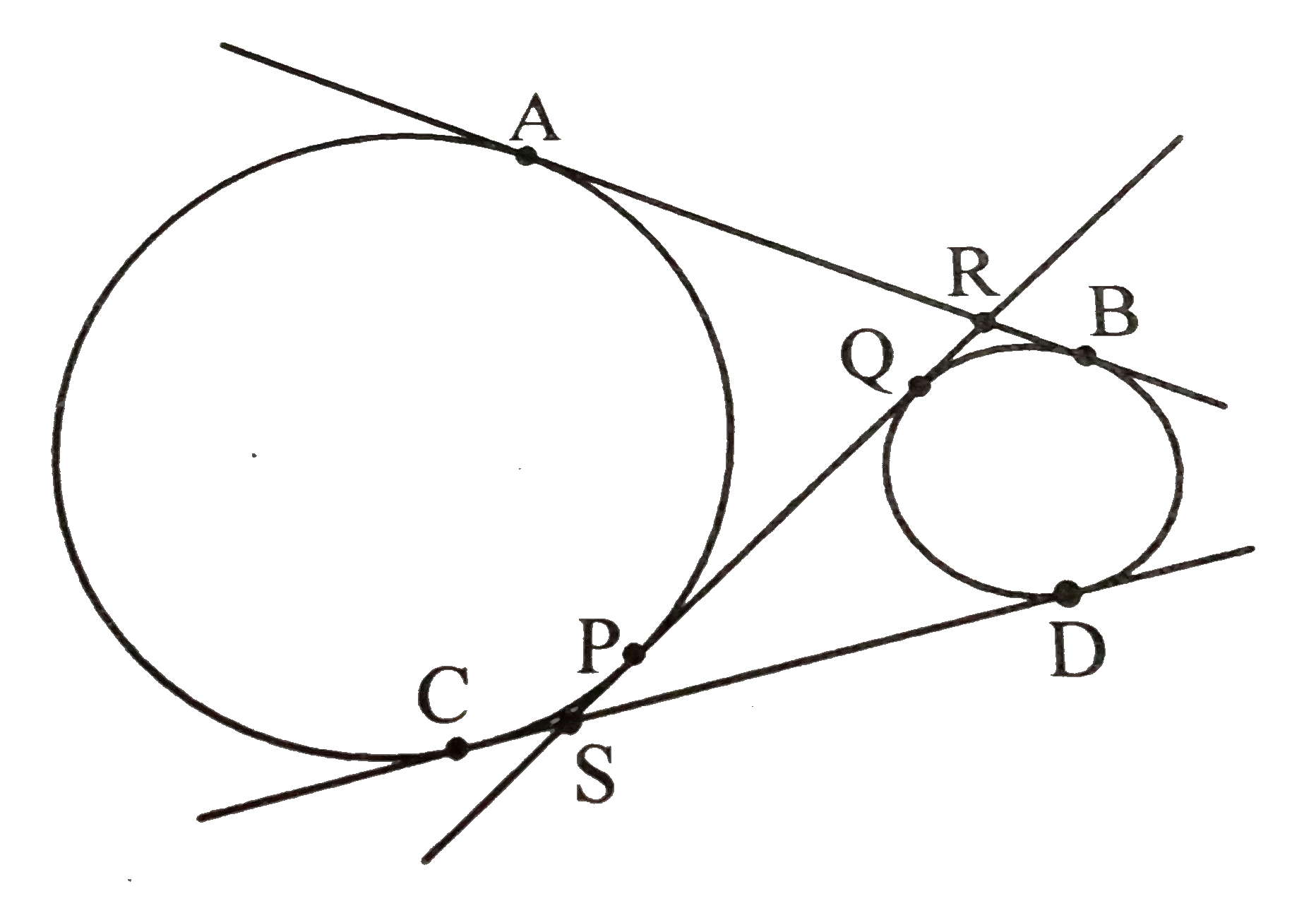 A8B9C10D11
A8B9C10D11Two circles touch each other externally at P. AB is a direct common tangent to the two circles, A and B are point of contact and ∠PAB=35∘. Then ∠ABP is
A35∘B55∘C65∘D75∘The two circles with radii 6 cm and 3 cm centered aat the point P and Q respectively A transvers common tangent AC to the both circles cuts line joining P and Q at the point B such that AB = 8 cm . Caculate the length (in cm) of PQ.
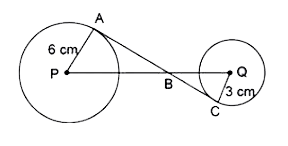 A5B10C15D20
A5B10C15D20
In the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove ∠CPA≅∠DPB.
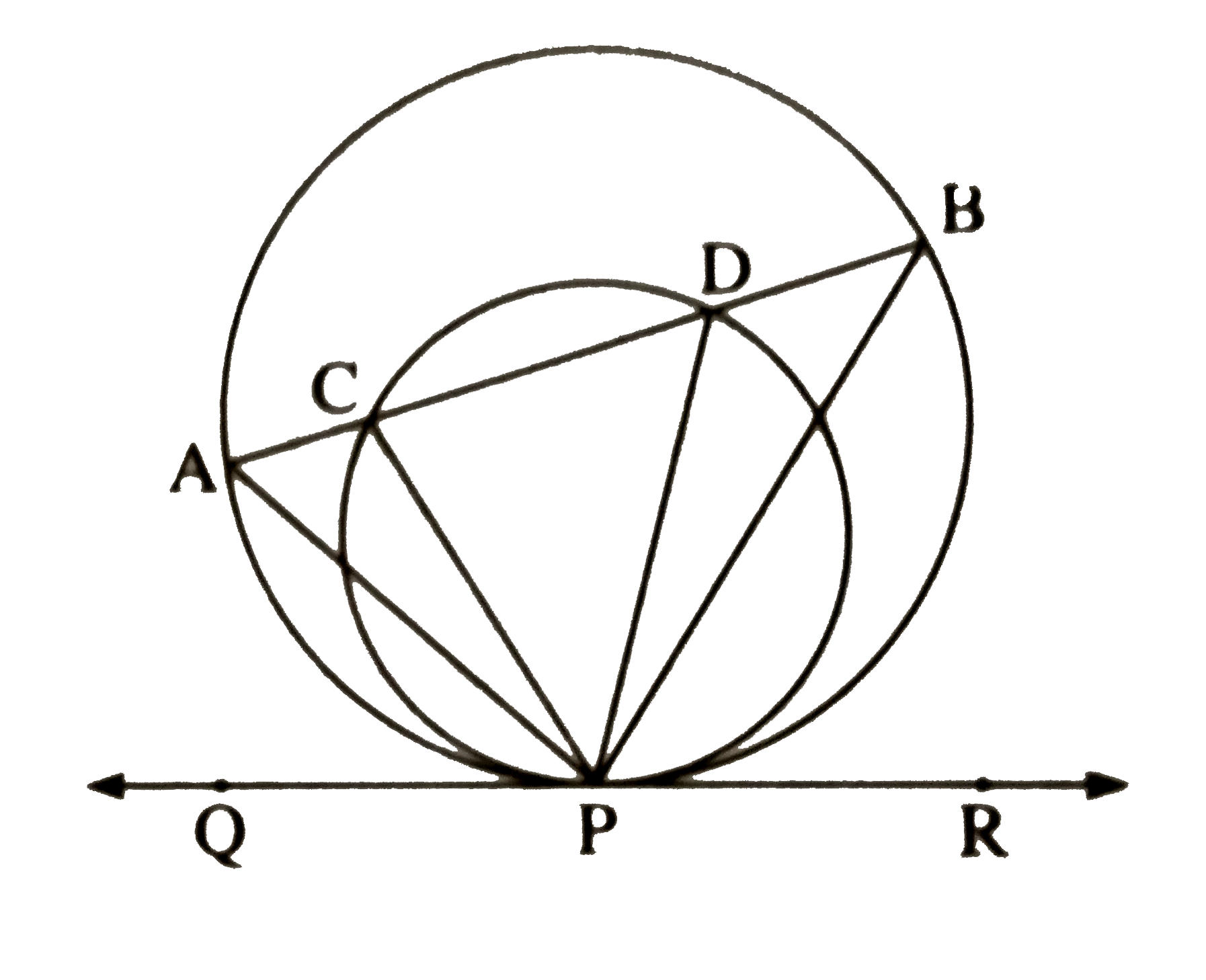
View SolutionAB and CD are common tangents to two circles which intersect each other at C as shown in the figure IF AB = 6cm , find CD.

View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

View SolutionLet PAB be a secant to a circle intersecting the circle at A and B. Let PT be the tangent segment. If PA = 9 cm and PT =12 cm, then what is AB equal to?
View SolutionThe two circles with radii 6 cm and 3 cm centered aat the point P and Q respectively A transvers common tangent AC to the both circles cuts line joining P and Q at the point B such that AB = 8 cm . Caculate the length (in cm) of PQ.

View Solution
