List ST touch the circle at P and QR is a diameter of the circle. If ∠RPT=50∘ then ∠SPQ will be-
40∘
60∘
80∘
100∘
To solve the problem, we need to find the angle ∠SPQ given that ST is a tangent to the circle at point P, QR is the diameter of the circle, and ∠RPT=50∘.
1. Identify the Given Information:
- ST is a tangent to the circle at point P.
- QR is the diameter of the circle.
- ∠RPT=50∘.
2. Use the Property of the Tangent:
- The angle between a tangent and a radius drawn to the point of tangency is 90∘. Therefore, ∠RPT+∠RPO=90∘.
- Since RPO is the radius at point P, we can write:
∠RPO=90∘−∠RPT=90∘−50∘=40∘.
3. Identify the Angles in Triangle PQR:
- QR is the diameter, so by the property of angles in a semicircle, ∠PQR=90∘.
- In triangle PQR, we have:
∠PQR+∠RQP+∠PRQ=180∘.
- Substituting the known values:
90∘+∠RQP+50∘=180∘.
- Simplifying this gives:
∠RQP=180∘−90∘−50∘=40∘.
4. Use the Alternate Segment Theorem:
- According to the alternate segment theorem, the angle ∠SPQ is equal to the angle ∠RQP.
- Therefore, we can conclude:
∠SPQ=∠RQP=40∘.
Final Answer:
∠SPQ=40∘.
- ST is a tangent to the circle at point P.
- QR is the diameter of the circle.
- ∠RPT=50∘.
- The angle between a tangent and a radius drawn to the point of tangency is 90∘. Therefore, ∠RPT+∠RPO=90∘.
- Since RPO is the radius at point P, we can write:
∠RPO=90∘−∠RPT=90∘−50∘=40∘.
- QR is the diameter, so by the property of angles in a semicircle, ∠PQR=90∘.
- In triangle PQR, we have:
∠PQR+∠RQP+∠PRQ=180∘.
- Substituting the known values:
90∘+∠RQP+50∘=180∘.
- Simplifying this gives:
∠RQP=180∘−90∘−50∘=40∘.
- According to the alternate segment theorem, the angle ∠SPQ is equal to the angle ∠RQP.
- Therefore, we can conclude:
∠SPQ=∠RQP=40∘.
∠SPQ=40∘.
Topper's Solved these Questions
Similar Questions
In the given figure A,B is a chord of the circle and AOC is its diameter ,such that ∠ACB=50∘ .If AT is the tangent to the circle at the point A, then ∠BAT is equal to :

View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View Solution
Knowledge Check
List ST touch the circle at P and QR is a diameter of the circle. If ∠RPT=50∘ then ∠SPQ will be-
A40∘B60∘C80∘D100∘PQ is tangent at a point R of the circle with centre O. If ST is a diameter of the circle and ∠TRQ=30∘ find ∠PRS
A30∘B60∘C45∘D120∘In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
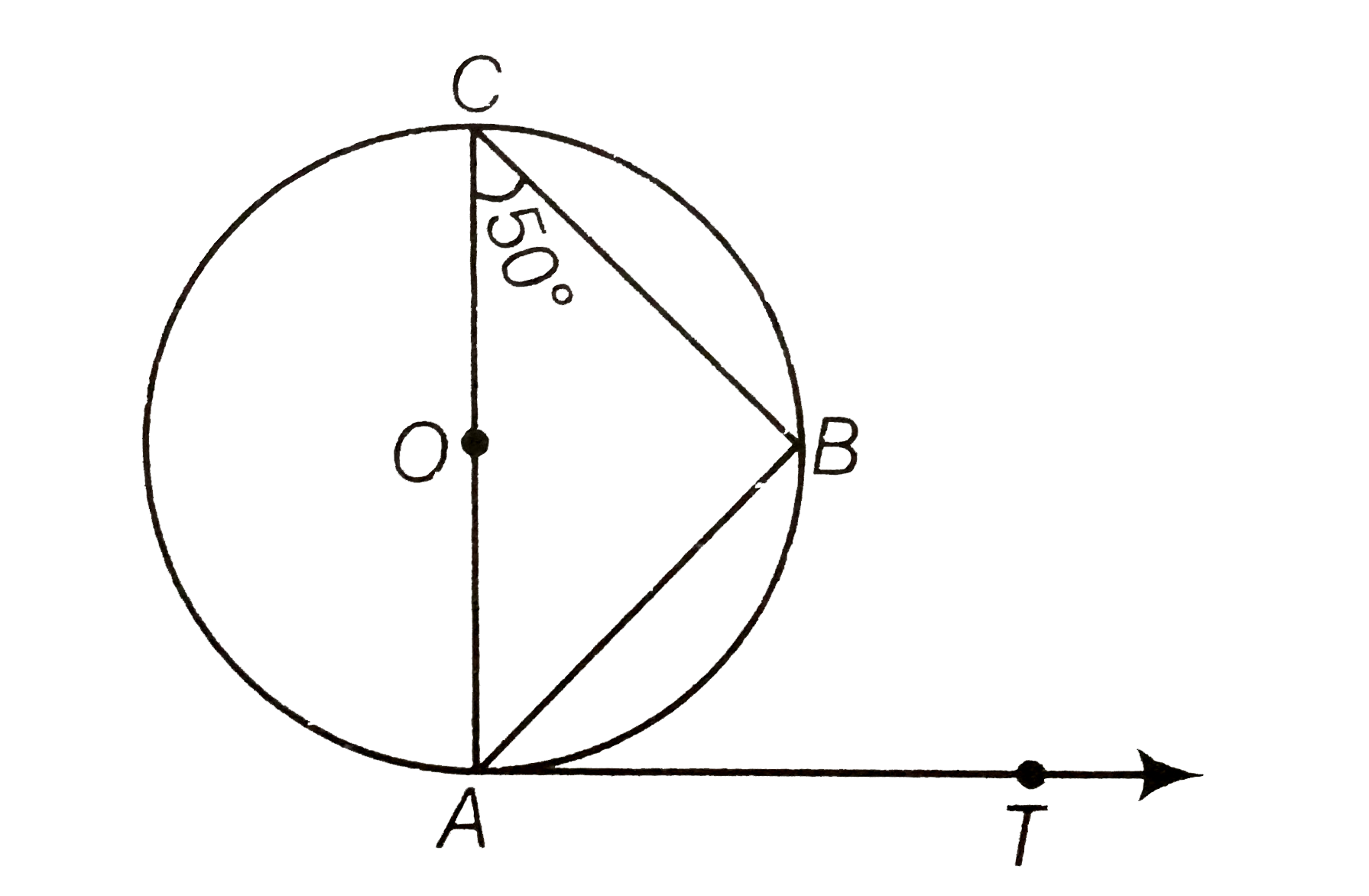 A45∘B60∘C50∘D55∘
A45∘B60∘C50∘D55∘
In the adjoning figure O is the centre of the circle and AB is the diameter. Tangent PQ touches the circle at D. ∠BDQ=48∘. Find the ratio of angleDBA:angleDCB.
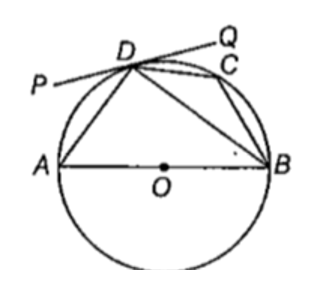
View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=50∘ then find ∠AOC
View SolutionPQRS is a cyclic uadrilateral such that PR is the diameter of the circle. If ∠QPR=50∘ and ∠SPR=60∘, then ∠QRS=…….
View SolutionThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
View SolutionThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
View Solution
