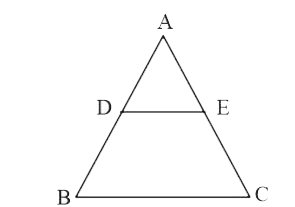
ABC is a triangle in which DE||BC and AD:DB = 5:4. Then DE:BC is
4:9
5:9
4:5
9:5
To solve the problem, we will use Thales' theorem, which states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
1. Identify the Given Ratios:
We are given that AD:DB=5:4. This means we can express AD and DB in terms of a variable x:
- Let AD=5x
- Let DB=4x
2. Calculate the Total Length of AB:
Since AB is the sum of AD and DB:
AB=AD+DB=5x+4x=9x
3. Apply Thales' Theorem:
According to Thales' theorem, since DE∥BC, we have the following proportionality:
ADAB=DEBC
4. Substitute the Known Values:
Substitute the values we have for AD and AB:
5x9x=DEBC
5. Simplify the Ratio:
The x cancels out:
59=DEBC
6. Conclusion:
Thus, the ratio DE:BC is:
DE:BC=5:9
Final Answer:
The ratio DE:BC is 5:9.
We are given that AD:DB=5:4. This means we can express AD and DB in terms of a variable x:
- Let AD=5x
- Let DB=4x
Since AB is the sum of AD and DB:
AB=AD+DB=5x+4x=9x
According to Thales' theorem, since DE∥BC, we have the following proportionality:
ADAB=DEBC
Substitute the values we have for AD and AB:
5x9x=DEBC
The x cancels out:
59=DEBC
Thus, the ratio DE:BC is:
DE:BC=5:9
The ratio DE:BC is 5:9.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In ΔABC,D and E are the points on sides AB and BC respectively such that DE || AC. If AD : DB = 5 : 3, then what is the ratio of the area of ΔBDE to that of the trapezium ACED ?
A1:6B4:25C9:55D9:64
If triangle ABC is similar to triangle DEF such that 2AB = DE and BC = 8 cm then EF is .
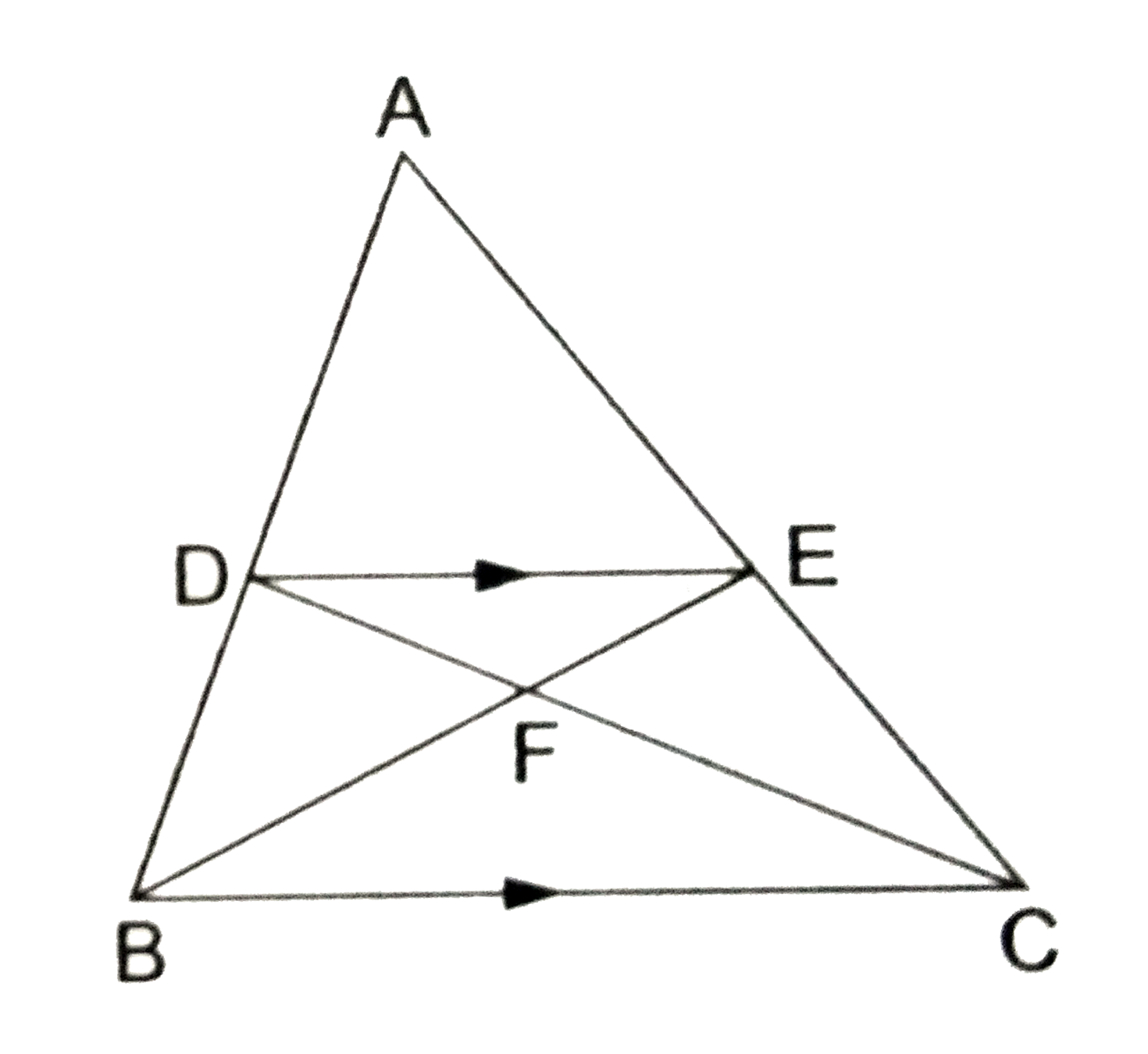
View SolutionIn the given figure DE∣∣BCandAD:DB=5:4
Find the ratio ar(ΔDEF):ar(ΔCFB)
View SolutionIn the given figure DE||BC and AD :DB = 5 : 3, what is the value of (DE:BC)?

View SolutionIn a triangle ABC , D & E are two points on sides AB and AC such that DE∣∣BC and AD:DB=3:5. Find the ratio of area of ΔADE to the area of trapezium BDEC.
View SolutionIn triangle ABC, DE∣∣BCandADDB=3(5) . If AC = 4.8 cm .Find AE.
View SolutionIn figure DE∣∣BC,andAD=12AB. IF BC=4.5cm, find DE.
View SolutionIn △ABC, D and E are the points on sides AB and BC respectively such that DE || AC. If AD : DB = 5 : 3, then what is the ratio of the area of △BDE to that of the trapezium ACED?
View Solution