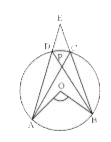
The point of intersection for the diagonals AC and BD of the cyclic quadrilateral ABC is P. If and , the measure of is
To find the measure of angle ADB in the cyclic quadrilateral ABC, we can follow these steps:
1. Identify the Given Angles:
- We have angle APB = 64° and angle CBD = 28°.
2. Use Vertical Angles:
- Since angles APB and CPD are vertical angles, angle CPD is also 64°.
3. Identify Angle ACB:
- In a cyclic quadrilateral, the angles subtended by the same chord are equal. Therefore, angle ACB (which is opposite to angle CBD) is also 28°.
4. Calculate Angle BPD:
- The angles on a straight line add up to 180°. Therefore, angle BPD can be calculated as:
Angle BPD=180°−Angle APB=180°−64°=116°
5. Use the Triangle Sum Theorem in Triangle ADP:
- In triangle ADP, the sum of the angles is 180°:
Angle ADB+Angle APB+Angle ADP=180°
- We already know angle APB = 64° and angle ADP = 116° (from step 4). Let angle ADB be denoted as x:
x+64°+28°=180°
6. Solve for Angle ADB:
- Rearranging the equation gives:
x+64°+28°=180°
x+92°=180°
x=180°−92°=88°
Thus, the measure of angle ADB is 36°.
- We have angle APB = 64° and angle CBD = 28°.
- Since angles APB and CPD are vertical angles, angle CPD is also 64°.
- In a cyclic quadrilateral, the angles subtended by the same chord are equal. Therefore, angle ACB (which is opposite to angle CBD) is also 28°.
- The angles on a straight line add up to 180°. Therefore, angle BPD can be calculated as:
Angle BPD=180°−Angle APB=180°−64°=116°
- In triangle ADP, the sum of the angles is 180°:
Angle ADB+Angle APB+Angle ADP=180°
- We already know angle APB = 64° and angle ADP = 116° (from step 4). Let angle ADB be denoted as x:
x+64°+28°=180°
- Rearranging the equation gives:
x+64°+28°=180°
x+92°=180°
x=180°−92°=88°
Topper's Solved these Questions
Similar Questions
Knowledge Check
The point of intersection for the diagonals AC and BD of the cyclic quadrilateral ABC is P. If ∠APB=64∘ and ∠CBD=28∘, the measure of ∠ADB is
A32∘B36∘C56∘D28∘ABCD is a cyclic quadrilateral. Diagonals AC and BD meets at P. If ∠APB=110∘ and ∠CBD=30∘, then ∠ADB measures
A55∘B30∘C70∘D80∘ABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is:
Aa) 50∘Bb) 35∘Cc) 55∘Dd) 30∘
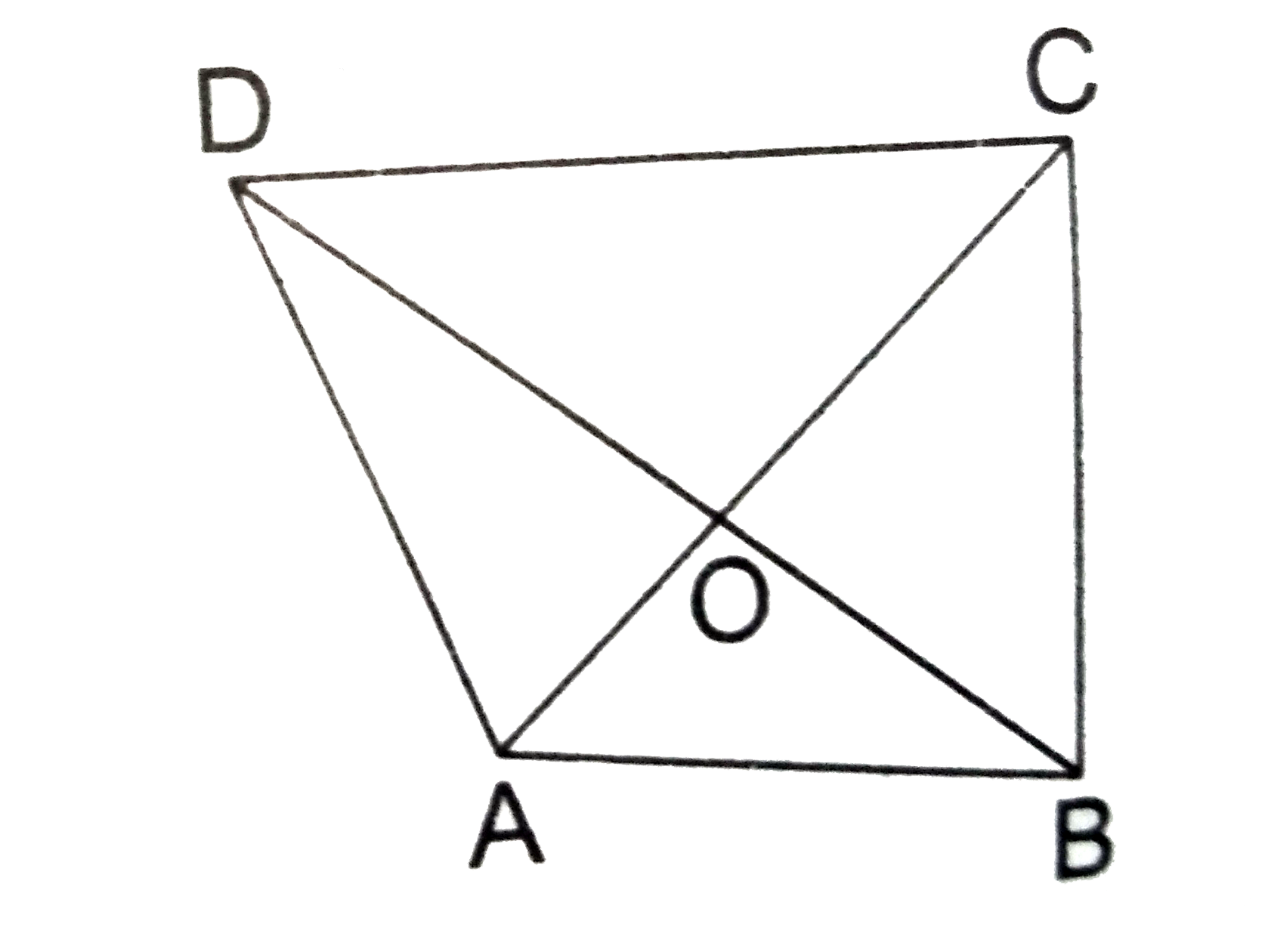
In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
View SolutionThe diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that
View SolutionThe diagonals AC and BD of a cyclic quadrilateral ABCD inter sect each other at the point P. Then, it is always true that
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
View SolutionABCD is a cycle quadrilateral. Diagonals BD and AC intersect each other at E. If ∠BEC=128∘ and ∠ECD=25∘ then what is the measure of ∠BAC ?
View Solution