A particle is thrown over a triangle from one end of horizontal base and grazing over the vertex falls on the other end of the base. If α,β are the base angles and θ the angle of projection, then
tanθ=tanα−tanβ
tanθ=tanβ−tanα
tanθ=tanα+tanβ
None of these
The correct Answer is:C
To solve the problem, we need to analyze the projectile motion of a particle thrown over a triangle. The triangle has a horizontal base with angles α and β at the ends, and the particle grazes the vertex of the triangle before landing on the other end of the base.
1. Understand the Geometry:
- Let the triangle have a horizontal base with points A and B at the ends, and vertex C at the top. The angles at points A and B are α and β respectively.
2. Identify the Projectile Motion:
- The particle is projected from point A with an initial velocity u at an angle θ with the horizontal. It grazes point C (the vertex) and lands at point B.
3. Define the Coordinates:
- Let the horizontal distance from A to B be R (the range). The height at point C (the vertex) can be denoted as h.
4. Use the Tangent Function:
- The height h can be expressed in terms of the angles:
h=Rtanα(for angle α)
h=Rtanβ(for angle β)
- Since both expressions equal h, we can set them equal to each other:
Rtanα=Rtanβ
5. Relate the Angles:
- The particle grazes the vertex C, which means that the total vertical distance covered by the projectile when it reaches point C must equal the height of the triangle:
h=Rtanθ
6. Combine the Equations:
- From the previous steps, we have:
Rtanθ=Rtanα+Rtanβ
- Dividing through by R (assuming R≠0):
tanθ=tanα+tanβ
7. Conclusion:
- The relationship between the angles of projection and the base angles of the triangle is given by:
tanθ=tanα+tanβ
Final Answer:
Thus, the relationship derived from the problem is:
tanθ=tanα+tanβ
- Let the triangle have a horizontal base with points A and B at the ends, and vertex C at the top. The angles at points A and B are α and β respectively.
- The particle is projected from point A with an initial velocity u at an angle θ with the horizontal. It grazes point C (the vertex) and lands at point B.
- Let the horizontal distance from A to B be R (the range). The height at point C (the vertex) can be denoted as h.
- The height h can be expressed in terms of the angles:
h=Rtanα(for angle α)
h=Rtanβ(for angle β)
- Since both expressions equal h, we can set them equal to each other:
Rtanα=Rtanβ
- The particle grazes the vertex C, which means that the total vertical distance covered by the projectile when it reaches point C must equal the height of the triangle:
h=Rtanθ
- From the previous steps, we have:
Rtanθ=Rtanα+Rtanβ
- Dividing through by R (assuming R≠0):
tanθ=tanα+tanβ
- The relationship between the angles of projection and the base angles of the triangle is given by:
tanθ=tanα+tanβ
Thus, the relationship derived from the problem is:
tanθ=tanα+tanβ
Similar Questions
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
View SolutionA particle is projected over a traingle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If α and β be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ.
View Solution
Knowledge Check
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30∘and60∘ be the base angles and θ the angle of projection then tanθ is
A2√3B4√3C13D3
A particle is projected over a triangle from one extremity of its horizontal base. Grazing over the vertex, it falls on the other extremity of the base. If aandb are the base angles of the triangle and θ the angle of projection, prove that tanθ=tan∝+tanβ.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionIn an isosceles triangle if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle
View SolutionIn an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
Let each base angle be x in an isosceles △ABC
Then vertex angle be 2(x+x)=4x
Since sum of angles of a triangle is 1800
Hence,4x+x+x=1800
6x=1800
⇒x=300
Angles are 300,300,1200
View SolutionA projectile is fired from the base of cone shaped hill. The projectle grazes the vertex and strikes the hill again at the base. If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then tanθtanα is:
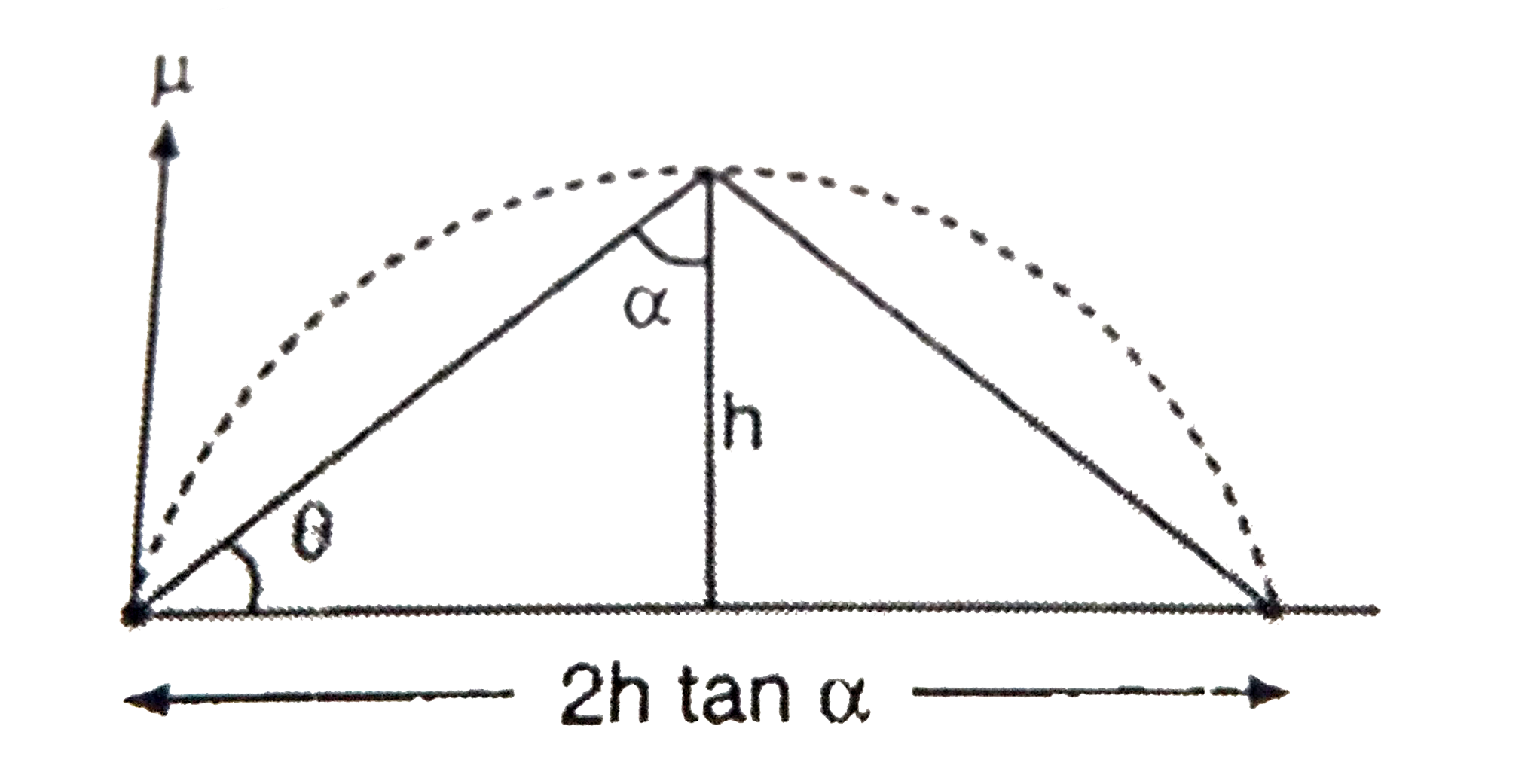
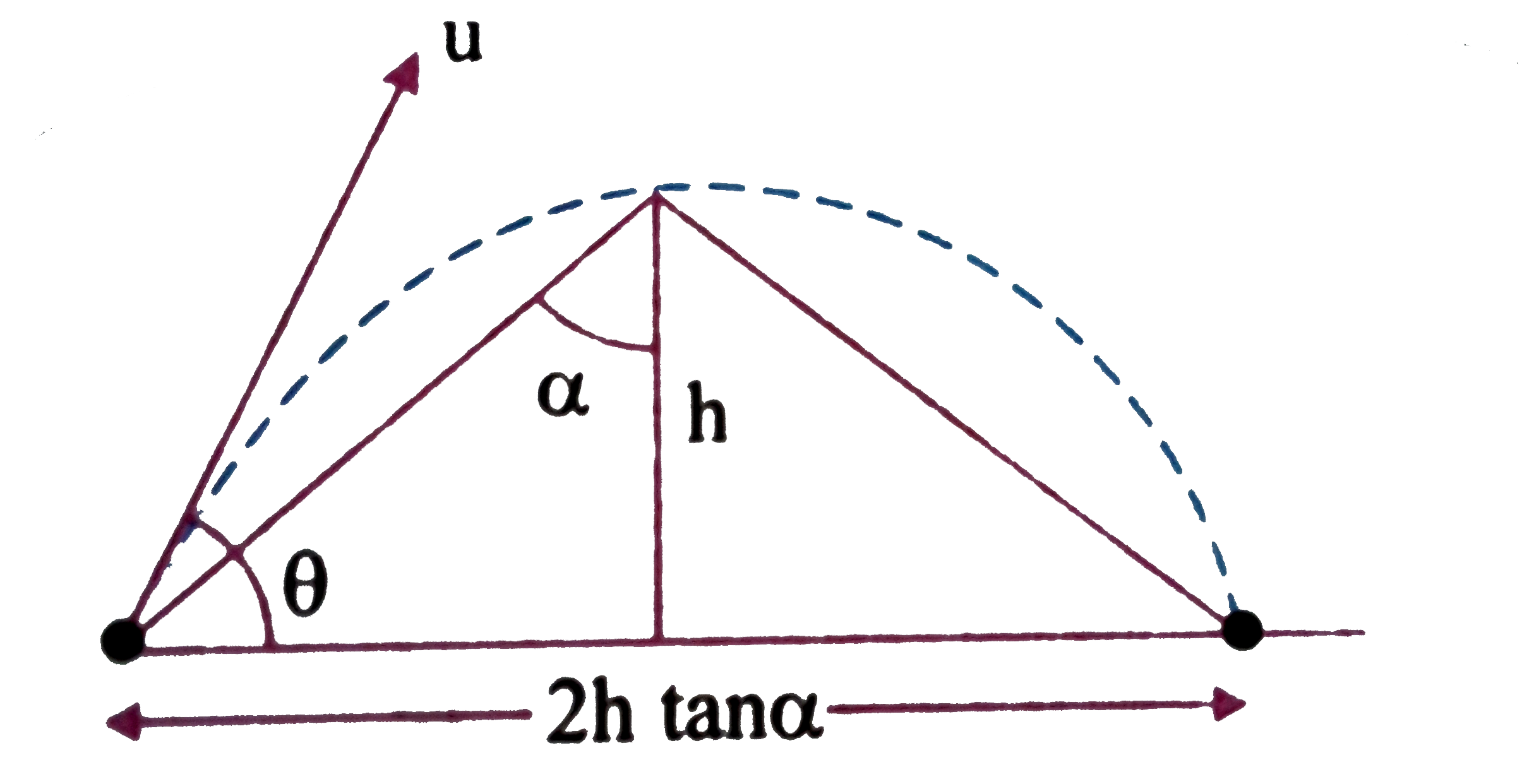
View SolutionA projectile is fired from the base of coneshaped hill. The projectile grazes the vertex and strikes the hill again at the base.If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then then θtanθis
View SolutionIf in an isosceles triangle, each of the base angles is 40°, then the triangle is
View Solution
