The ratio of the greatest range up an inclined plane through the point of projection and the distance through which a particle falls freely during the corresponding time of flight is
2
12
1
3
The correct Answer is:C
Similar Questions
A particle is projected so as to have a range R on a horizontal plane through the point of projection and the greatest height attained by it is h. The maximum horizontal range with this velocity of projection is
2h+R28h or u={2g(h+R216h)}1/2
View SolutionA particle projected with velcoity v0 strikes at right α plane through the point of projection .
View Solution
Knowledge Check
The horizontal range of an oblique projectile is equal to the distance through which a projectile has to fall freely from rest to acquire a velocity equal to the velocity of projection in magnitude. The angle of projection is
A75∘B60∘C45∘D30∘The ratio of the range of the particle and its maximum range in the inclined plane is:
A1:2B1:√2C1:√3D1:1
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Fig. 2 (EP). 26)
(a) Find an expression for range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) β at which range will be maximum.
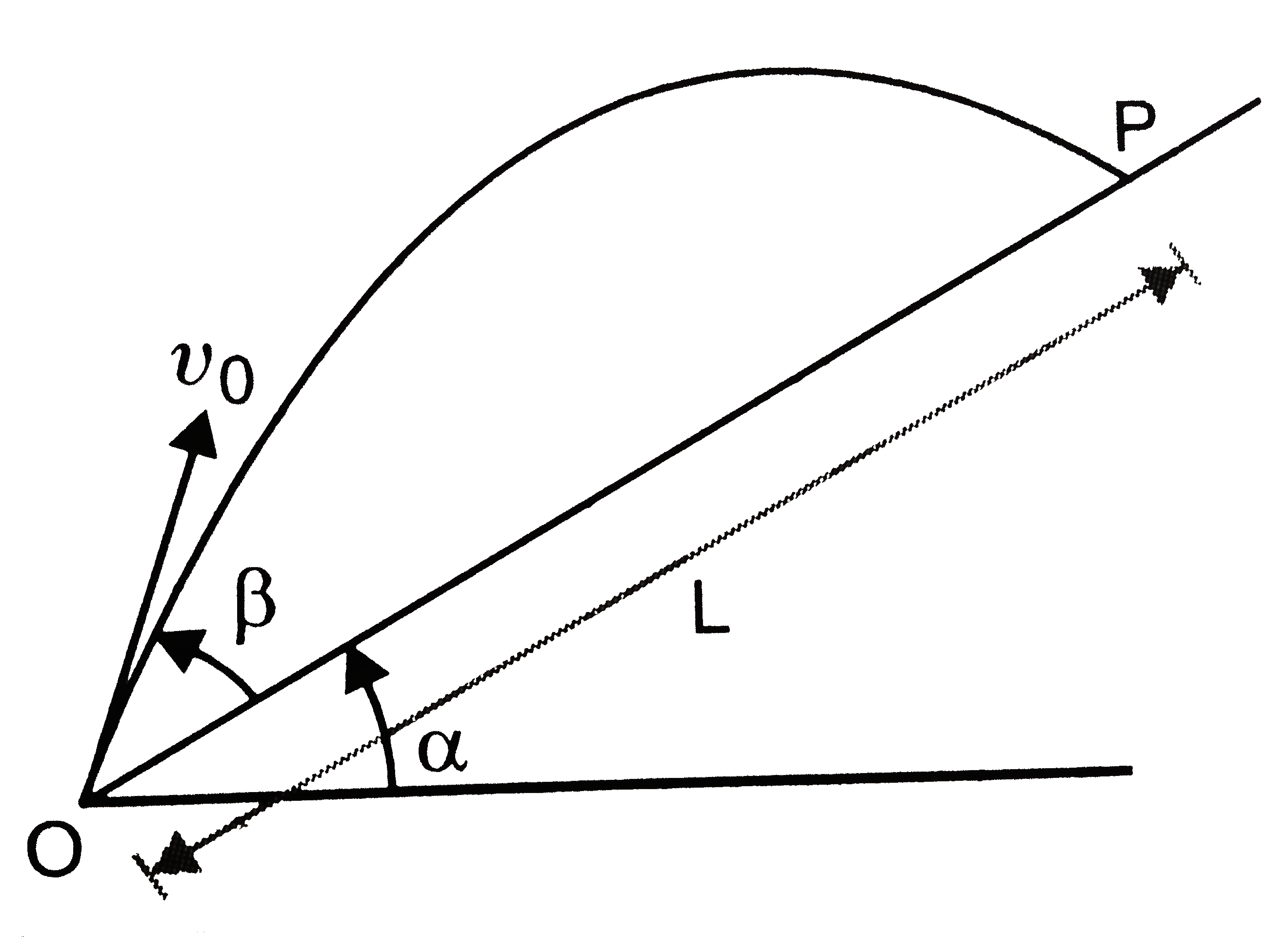
View SolutionA particle is projected in aer an angle β to a surface which itself is inclined at an angle α to the horixonta (Fig. 2 (EP). 26)
(a) Find an ecxpression for range on the plane surface (distanc eon the plance from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) β at which range will be maximum.

View SolutionThe horizontal range of an oblique projectile is equal to the distance through which a projectile has to fall freely from rest to acquire a velocity equal to the velocity of projection in magnitude. The angle of projection is
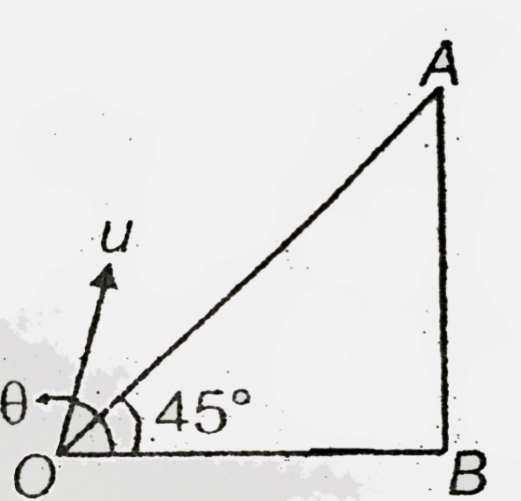
View SolutionA particles is projected from the foot of an inclined plane having inclination 45∘ , with the velocity u at angle θ(>45∘) with the horizontal in a vertical plane containing the line of greatest slope through the point of projection. Find the value of tanθ if the particle stikes the plane.
(i) Horizontally
(ii) Normally
View SolutionA parrticle projected with velocity u strikes at right angles a plane through the point of projection inclined at angle β to the horizon. Show that the height of the point struck above the horizontal plane through the point of projection is 2u2g.sin2β1+3sin2β and that the time of flight up to that instant is t=2ug√1+3sin2β.
View SolutionA body is projected up with a speed v0 along the line of greatest slope of an inclined plane of angle of inclination β. If the body collides elastically perpendicular to the inclined plane, find the time after which the body passes through its point of projection.
View Solution
