A particles is projected from the foot of an inclined plane having inclination $45^{\circ}$ , with the velocity u at angle $θ (> 45^{\circ})$ with the horizontal in a vertical plane containing the line of greatest slope through the point of projection. Find the value of $tan θ$ if the particle stikes the plane.
(i) Horizontally
(ii) Normally

Video Solution

Text Solution

Verified by Experts

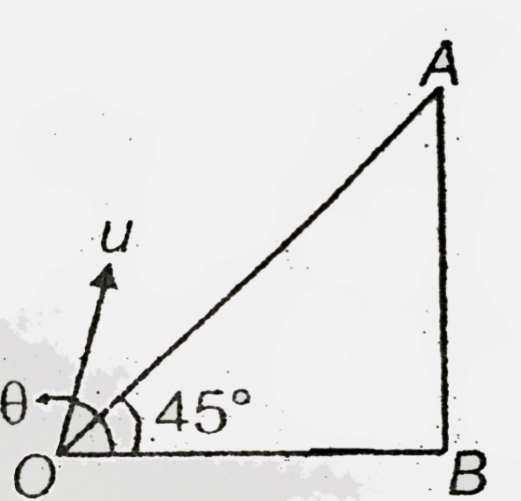
Let A be the point where the particel strikes the plane after time t.
and OB = AB =h
$\Rightarrow O A = h \sqrt{2}$
(i) As the paticle strikes the plane horinzontally, vetical component of its velocity at A will be zero.
For horizontal motion.
$O B = (u cos θ) t \Rightarrow h = u cos θ t$
For vertical motion from equation v = u + at
$0 = u sin θ - >$
$or u sin θ = gt$
again, BP $= (u sin θ) t - \frac{1}{2} {gt}^{2}$
$h = (U sin θ) - \frac{1}{2} {gt}^{2}$
From equations (i),(ii) and (iii)
$u cos θ t = u sin θ t - \frac{1}{2} (u sin t e h t a) t$
$\Rightarrow tan θ = 2$
(ii) As the particle hits the plane normally, component of its velocity parallel to the plane at this instant will be zero and displancement perpendicular to the plane will be zero.
for the motion along the plane,.
From v = u +at
$0 = u cos (θ - 45^{\circ}) - g {sin 45}^{\circ} t$
$R i g h t a r r w u cos (θ - 45^{\circ}) = \frac{g}{\sqrt{2}} t$
Again , for the motion perpendicular to the plane from s $= u t + \frac{1}{2} a t^{2}$
$0 = u sin (θ - 45^{\circ}) t - \frac{1}{2} g {cos 45}^{\circ} t^{2}$
$\Rightarrow t = \frac{2 \sqrt{2} u}{g} sin (θ - 45^{\circ})$

From equation (i) & (ii)
$u cos (θ - 45^{\circ}) = \frac{g}{\sqrt{2}} [\frac{2 \sqrt{2} u}{g} sin (θ - 45^{\circ})]$
$\Rightarrow u cos (θ - 45^{\circ}) = 2 u sin (θ - 45^{\circ})$
$\Rightarrow tan (θ - 45^{\circ}) = \frac{1}{2}$
$\Rightarrow \frac{tan θ - 1}{1 + tan θ} = \frac{1}{2}$
$\Rightarrow tan θ = 3$

|

Updated on:21/07/2023

Class 12 PHYSICS MOTION IN A PLANE

Topper's Solved these Questions

Similar Questions

AAKASH INSTITUTE ENGLISH-MOTION IN A PLANE-Assignement section -J (Aakash Challengers Questions)

Home
Ask Doubt
Profile