The centre of a wheel rolling on a plane surface moves with a speed . A particle on the rim of the wheel at the same level as the centre will be moving at a speed . Then the value of x is ______ .
To solve the problem, we need to determine the speed of a particle on the rim of a wheel that is rolling on a plane surface, given that the center of the wheel moves with a speed v0.
1. Understanding the Motion of the Wheel:
- The wheel is rolling without slipping on a plane surface. The center of the wheel moves with a constant speed v0.
2. Angular Velocity Relation:
- The angular velocity ω of the wheel is related to the linear speed v0 by the formula:
ω=v0R
where R is the radius of the wheel.
3. Velocity of the Particle on the Rim:
- A particle on the rim of the wheel at the same level as the center has two components of velocity:
- The linear velocity of the center of the wheel, which is v0 (horizontal direction).
- The tangential velocity due to the rotation of the wheel, which is given by:
vtangential=ωR=v0
(This tangential velocity is directed perpendicular to the radius at the point where the particle is located.)
4. Components of Velocity:
- The velocity of the particle can be represented as:
- v0 in the horizontal direction (due to the center of the wheel).
- v0 in the vertical direction (due to the tangential motion of the wheel).
5. Resultant Velocity Calculation:
- Since the two components of velocity are perpendicular to each other, we can use the Pythagorean theorem to find the resultant speed v of the particle:
v=√(v0)2+(v0)2=√2v20=v0√2
6. Relating to the Given Speed:
- The problem states that the speed of the particle is also given as √xv0. We can equate this to our derived speed:
√xv0=v0√2
7. Solving for x:
- Dividing both sides by v0 (assuming v0≠0):
√x=√2
- Squaring both sides gives:
x=2
Final Answer:
The value of x is 2.
- The wheel is rolling without slipping on a plane surface. The center of the wheel moves with a constant speed v0.
- The angular velocity ω of the wheel is related to the linear speed v0 by the formula:
ω=v0R
where R is the radius of the wheel.
- A particle on the rim of the wheel at the same level as the center has two components of velocity:
- The linear velocity of the center of the wheel, which is v0 (horizontal direction).
- The tangential velocity due to the rotation of the wheel, which is given by:
vtangential=ωR=v0
(This tangential velocity is directed perpendicular to the radius at the point where the particle is located.)
- The velocity of the particle can be represented as:
- v0 in the horizontal direction (due to the center of the wheel).
- v0 in the vertical direction (due to the tangential motion of the wheel).
- Since the two components of velocity are perpendicular to each other, we can use the Pythagorean theorem to find the resultant speed v of the particle:
v=√(v0)2+(v0)2=√2v20=v0√2
- The problem states that the speed of the particle is also given as √xv0. We can equate this to our derived speed:
√xv0=v0√2
- Dividing both sides by v0 (assuming v0≠0):
√x=√2
- Squaring both sides gives:
x=2
The value of x is 2.
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - A)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - B)
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
The centre of the wheel rolling on a plane surface moves with velocity v0. A particle on the rim of the wheel at same level as the centre will be √xv0. Find x
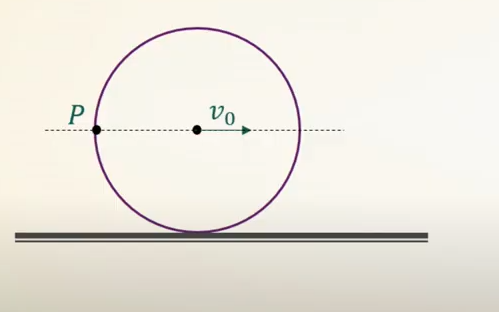
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View Solution
Knowledge Check
The centre of a wheel rolling on a plaen surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
AZeroBv0C√2v0D2v0The centre of a wheel rolling on a plaen surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
AZeroBv0C√2v0D2v0The centre of a wheel rolling on a plaen surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
AZeroBv0C√2v0D2v0
A sphere of mass m rolls on a plane surface.Find its kinetic energy t an instant when its centre moves with speed v.
View SolutionA dust particle lying at the rim of a wheel has an angular speed of 22 rad/s. Find the time period.
View SolutionConsider a wheel of a bicycle rolling on a level road at a liner speed v0 figure.

View SolutionA wheel ios rolling without sliding on a horizontal surface. The centre of the wheelk moves with a constant speed v0. Consider a point P on the rim which is at the top at time t=0. The square of speed of point P is plooted against time t. The correct plot is (R is radius of the wheel)
View SolutionA particle is moving in a circle of radius R with constant speed v, if radius is double then its centripetal force to keep the same speed should be
View Solution
