In a U-tube diamter of two limbs are 0.5 cm and 1 cm respectively and tube has filled with water (T=72dyne/cm) then liquid level difference between two limbs will be
0.5 cm
0.25 cm
0.293 cm
none of these
The correct Answer is:C
To solve the problem of finding the liquid level difference between the two limbs of a U-tube, we can follow these steps:
1. Identify the Given Values:
- Diameter of limb 1 (d1) = 0.5 cm
- Diameter of limb 2 (d2) = 1 cm
- Surface tension (T) = 72 dyne/cm
2. Calculate the Cross-Sectional Areas:
- The cross-sectional area (A) of a circular tube is given by the formula:
A=πd24
- For limb 1 (A1):
A1=π(0.5)24=π×0.254=π16 cm2
- For limb 2 (A2):
A2=π(1)24=π4 cm2
3. Set Up the Equations for Each Limb:
- The weight of the liquid column in limb 1 is balanced by the surface tension:
T⋅πd1=A1⋅x⋅ρ⋅g
- The weight of the liquid column in limb 2 is also balanced by the surface tension:
T⋅πd2=A2⋅y⋅ρ⋅g
4. Substituting the Values into the Equations:
- For limb 1:
72⋅π⋅0.5=π16⋅x⋅1⋅980
Simplifying gives:
36π=π16⋅980x
Canceling π and solving for x:
36=980x16⟹x=36⋅16980≈0.5877 cm
- For limb 2:
72⋅π⋅1=π4⋅y⋅1⋅980
Simplifying gives:
72π=π4⋅980y
Canceling π and solving for y:
72=980y4⟹y=72⋅4980≈0.2938 cm
5. Calculate the Liquid Level Difference:
- The difference in liquid levels (x - y) is:
x−y=0.5877−0.2938≈0.2939 cm
Final Answer:
The liquid level difference between the two limbs is approximately 0.2939 cm.
---
- Diameter of limb 1 (d1) = 0.5 cm
- Diameter of limb 2 (d2) = 1 cm
- Surface tension (T) = 72 dyne/cm
- The cross-sectional area (A) of a circular tube is given by the formula:
A=πd24
- For limb 1 (A1):
A1=π(0.5)24=π×0.254=π16 cm2
- For limb 2 (A2):
A2=π(1)24=π4 cm2
- The weight of the liquid column in limb 1 is balanced by the surface tension:
T⋅πd1=A1⋅x⋅ρ⋅g
- The weight of the liquid column in limb 2 is also balanced by the surface tension:
T⋅πd2=A2⋅y⋅ρ⋅g
- For limb 1:
72⋅π⋅0.5=π16⋅x⋅1⋅980
Simplifying gives:
36π=π16⋅980x
Canceling π and solving for x:
36=980x16⟹x=36⋅16980≈0.5877 cm
72⋅π⋅1=π4⋅y⋅1⋅980
Simplifying gives:
72π=π4⋅980y
Canceling π and solving for y:
72=980y4⟹y=72⋅4980≈0.2938 cm
- The difference in liquid levels (x - y) is:
x−y=0.5877−0.2938≈0.2939 cm
The liquid level difference between the two limbs is approximately 0.2939 cm.
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Assertion & Reason)
32 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Comprehension based questions)
24 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Fluid Statics)
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
In a U-tube the radii of two columns are respectively r1andr2 and if a liquid of density d filled in it has level difference of h then the surface tension of the liquid is -

View SolutionWater is flowing through two horizontal pipes of different diameters which are connected together. The diameters of the two pipes are 3 cm and 6 cm respectively. If the speed of water in the narrower tube is 4ms−1. Then the speed of water in the wider tube is
View Solution
Knowledge Check
Two syringes of different cross-section (without needle filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston an larger piston are 1cm and 3cm respectively. If a force of 10N is applied to the smaller piston then the force exerted on the larger piston is
A30NB60 NC90 ND100 N
Water flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionTwo capillary tubes of diameters 3.0mm and 6.0mm are joined together to form a U-tube open at both ends. If the U-tube is filled with water, what is the difference in its levels in the two limbs of the tube ? Surface tension of water at the temperature of the experiment is 7.3×102N/m. Take the angie of contact to be zero and density of water to be 103kg/m3(g=9.8m/s2)
View SolutionA vertical U-tube of uniform cross-section contains water jn both the arms. A 10 cm glycerine column (R.D. = 1.2) is added to one of the limbs. The level difference between the two free surfaces in the two limbs wiil be
View SolutionA U−tube is made up of capillaries of bores 1mm and 2mm respectively. The tube is held vertically and partically filled with a liquid of surface tension 49dyne/cm and zero contact angle. Calculate the density of the liquid of the difference in the levels of the meniscus is 1.25cm.
View SolutionA U -tube in which the cross - sectional area of the limb on the left is one quarter, the limb on the right contains mercury (density13.6g/cm3). The level of mercury in the narrow limb is at a distance of 36 cm from the upper end of the tube. What will be the rise in the level of mercury in the right limb if the left limb is filled to the top with water ?
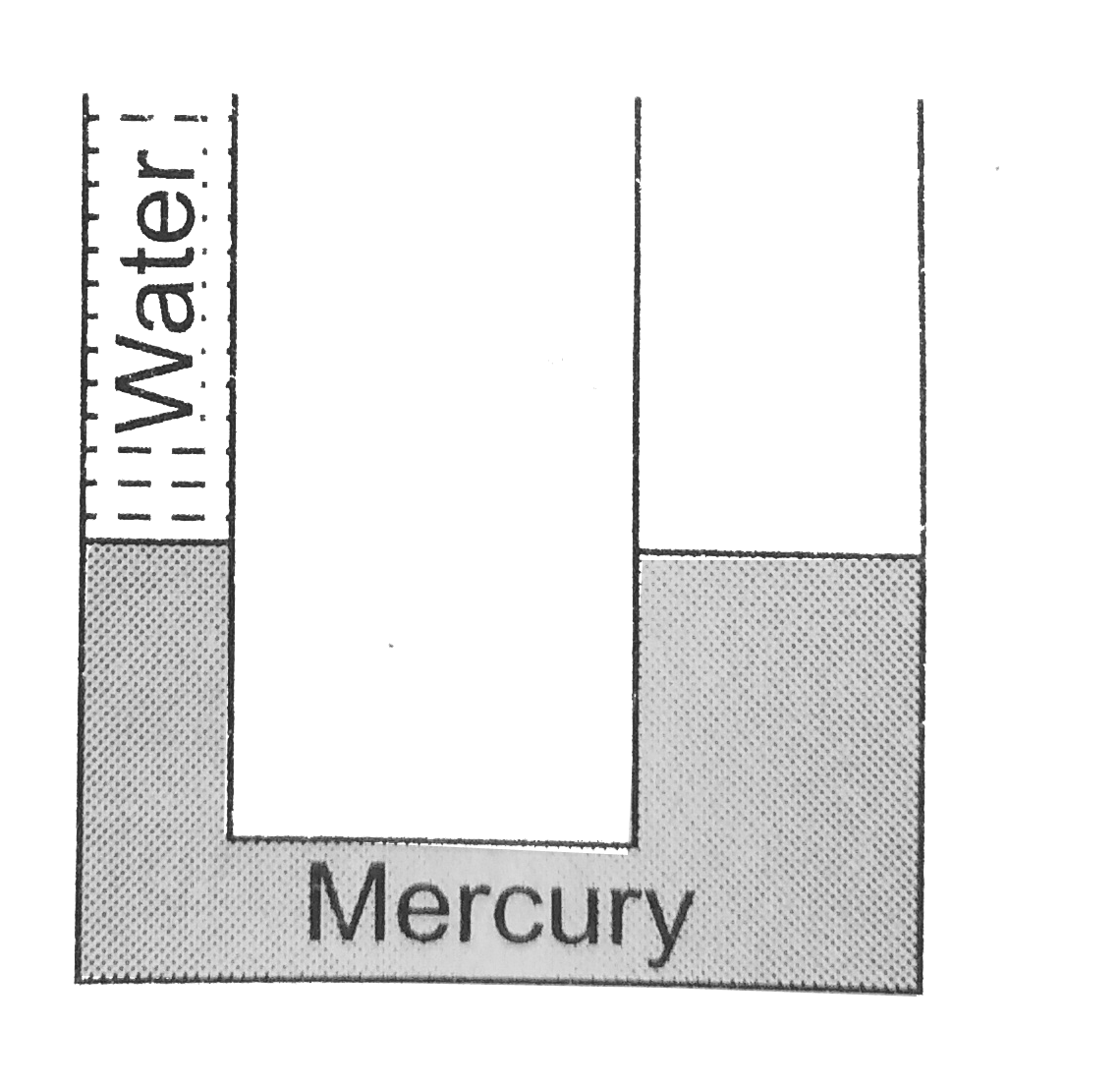
View SolutionIn the figure, the cross-sectional area of the smaller tube is a and that of the larger tube is 2a. A block of mass m is kept in the smaller tube having the base area that of the tube. The difference between water levels of the two tubes is

View Solution
