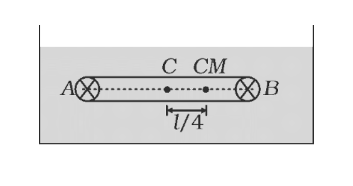
A non-uniform cylinder of mass m, length l and radius r has its centre of mass at a distance l/4 from the centre on the axis of the cylinder. The cylinder is kept in a liquid of uniform density $ρ$ . The moment of inertia of the rod about the centre of mass is I. The angular acceleration of point A relative to point B just after the rod is released from the position as shown in the figure is:

$\frac{π ρ g l^{2} r^{2}}{I}$

$\frac{π ρ g l^{2} r^{2}}{4 I}$

$\frac{π ρ g l^{2} r^{2}}{2 I}$

$\frac{3 π ρ g l^{2} r^{2}}{4 I}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video & image solution for A non-uniform cylinder of mass m, length l and radius r has its centre of mass at a distance l/4 from the centre on the axis of the cylinder. The cylinder is kept in a liquid of uniform density rho . The moment of inertia of the rod about the centre of mass is I. The angular acceleration of point A relative to point B just after the rod is released from the position as shown in the figure is: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

ALLEN-ELASTICITY, SURFACE TENSION AND FLUID MECHANICS-Exercise 2 (One or more than one correct answer)