A string of length L is stretched along the x-axis and is rigidly clamped at its two ends. It undergoes transverse vibration. If n an integer, which of the following relations may represent the shape of the string at any time :-
y=Asin(nπxL)cosωt
y=Asin(nπxL)sinωt
y=Acos(nπxL)cosωt
y=Acos(nπxL)sinωt
The correct Answer is:A, B
To solve the problem, we need to determine which of the given equations can represent the shape of a string undergoing transverse vibrations while being clamped at both ends. The boundary conditions are that the displacement y of the string must be zero at both ends, x=0 and x=L.
1. Understanding the Boundary Conditions:
- The string is clamped at both ends, which means that at x=0 and x=L, the displacement y must be zero:
y(0,t)=0andy(L,t)=0
2. Analyzing the First Equation:
- Let's consider the first equation:
y=Asin(nπxL)cos(ωt)
- Check the boundary conditions:
- At x=0:
y(0,t)=Asin(0)cos(ωt)=0
- At x=L:
y(L,t)=Asin(nπ)cos(ωt)=0
- Both conditions are satisfied, so this equation is valid.
3. Analyzing the Second Equation:
- Now consider the second equation:
y=Asin(nπxL)sin(ωt)
- Check the boundary conditions:
- At x=0:
y(0,t)=Asin(0)sin(ωt)=0
- At x=L:
y(L,t)=Asin(nπ)sin(ωt)=0
- Both conditions are satisfied, so this equation is also valid.
4. Analyzing the Third Equation:
- Now consider the third equation:
y=Acos(nπxL)cos(ωt)
- Check the boundary conditions:
- At x=0:
y(0,t)=Acos(0)cos(ωt)=Acos(ωt)(not 0)
- This does not satisfy the boundary condition at x=0, so this equation is invalid.
5. Analyzing the Fourth Equation:
- Finally, consider the fourth equation:
y=Acos(nπxL)sin(ωt)
- Check the boundary conditions:
- At x=0:
y(0,t)=Acos(0)sin(ωt)=Asin(ωt)(not 0)
- This does not satisfy the boundary condition at x=0, so this equation is also invalid.
Conclusion:
The valid equations that represent the shape of the string at any time are:
- y=Asin(nπxL)cos(ωt)
- y=Asin(nπxL)sin(ωt)
Final Answer:
The correct options are the first and second equations.
- The string is clamped at both ends, which means that at x=0 and x=L, the displacement y must be zero:
y(0,t)=0andy(L,t)=0
- Let's consider the first equation:
y=Asin(nπxL)cos(ωt)
- Check the boundary conditions:
- At x=0:
y(0,t)=Asin(0)cos(ωt)=0
- At x=L:
y(L,t)=Asin(nπ)cos(ωt)=0
- Both conditions are satisfied, so this equation is valid.
- Now consider the second equation:
y=Asin(nπxL)sin(ωt)
- Check the boundary conditions:
- At x=0:
y(0,t)=Asin(0)sin(ωt)=0
- At x=L:
y(L,t)=Asin(nπ)sin(ωt)=0
- Both conditions are satisfied, so this equation is also valid.
- Now consider the third equation:
y=Acos(nπxL)cos(ωt)
- Check the boundary conditions:
- At x=0:
y(0,t)=Acos(0)cos(ωt)=Acos(ωt)(not 0)
- This does not satisfy the boundary condition at x=0, so this equation is invalid.
- Finally, consider the fourth equation:
y=Acos(nπxL)sin(ωt)
- Check the boundary conditions:
- At x=0:
y(0,t)=Acos(0)sin(ωt)=Asin(ωt)(not 0)
- This does not satisfy the boundary condition at x=0, so this equation is also invalid.
The valid equations that represent the shape of the string at any time are:
- y=Asin(nπxL)cos(ωt)
- y=Asin(nπxL)sin(ωt)
The correct options are the first and second equations.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-03)31videos
WAVES AND OSCILLATIONS
- BOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[A]29videos
WAVES AND OSCILLATIONS
- BOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-01)53videos
WAVES AND OSCILLATIONS
- BOOK - ALLENCHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)51videos
SEMICONDUCTORS
Similar Questions
Light waves travels in vacuum along the X-axis. Which of the following may represent the wavefronts?
View SolutionA string of length 2L, obeying hooke's law, is stretched so that its extension is L. the speed of the transverse wave travelling on the string is v. If the string is further stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
View Solution
Knowledge Check
- Question 1 - Select One
One end of a taut string of length 3m along the x-axis is fixed at x=0. The speed of the waves in the string is 100ms−1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength(s) of these sationary waves is (are)
Ay(t)=Asin(2πx)6cos(50πt)3By(t)=Asin(πx)3cos(100πt)3Cy(t)=Asin(5πx)6cos(255πt)3Dy(t)=Asin(5πx)2cos250πt
A string of length 2x is stretched by 0.1 x and the velocity of a transverse wave along it is v. When it is stretched by 0.4x , the velocity of the wave is
View SolutionA string is rigidly tied at two ends and its equation of vibration is given by y=cos2πx. Then minimum length of string is
View SolutionA string of length 2L, obeying Hooke's Law, is stretched so that its extension is L. The speed of the tranverse wave travelling on the string is v. if the string is futher stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
View SolutionA sonometer strings AB of length 1m is stretched by a load and the tension T is adjusted so that the string resonates to a frequency of 1kHz. Any point P of the wire may be held fixed by use of a movable bridge that can slide along the base of sonometer.
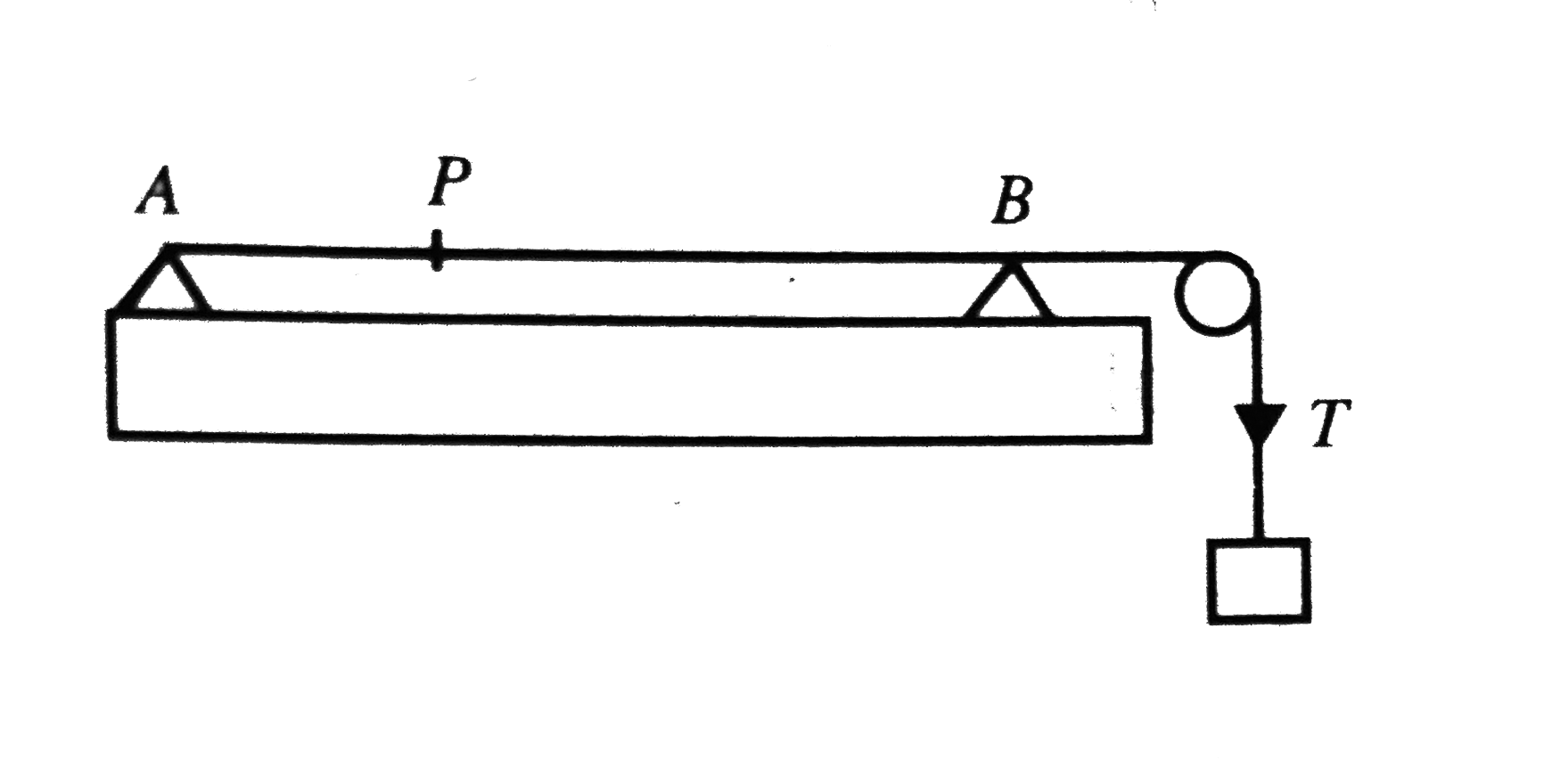 View Solution
View SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).
 View Solution
View SolutionA string of length L and mass M hangs freely from a fixed point . Calculate the velocity of the transverse wave along the string at any position.
(b)Calculate time taken by a transverse pulse to traverse the string.View SolutionA 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 220ms−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0.5 cm, write a suitable equation describing the motion.
View Solution

