Assertion:- For a particle moving along a straight line, if they velocity and acceleration have same sign, then the particle may be slowing down.
Reason:- For a moving particle speeding up and slowing down does not depend upon the angle between velocity and acceleration.
If both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are False.
The correct Answer is:D
To analyze the assertion and reason provided in the question, we will break down the concepts of velocity, acceleration, and their relationship in the context of motion along a straight line.
Step 1: Understanding the Assertion
The assertion states that for a particle moving along a straight line, if the velocity and acceleration have the same sign, then the particle may be slowing down.
- Analysis:
- If both velocity and acceleration are positive, the particle is speeding up.
- If both are negative, the particle is also speeding up (in the negative direction).
- Therefore, if the velocity and acceleration have the same sign, the particle cannot be slowing down; it is actually speeding up.
Step 2: Understanding the Reason
The reason states that for a moving particle, speeding up and slowing down does not depend upon the angle between velocity and acceleration.
- Analysis:
- The angle between velocity and acceleration does affect whether the particle speeds up or slows down.
- If acceleration has a component in the direction of velocity (same direction), the particle speeds up.
- If acceleration has a component opposite to the direction of velocity (opposite direction), the particle slows down.
- Thus, the statement that speeding up and slowing down does not depend on the angle is incorrect.
Conclusion
Both the assertion and reason are false. The correct conclusion is that if velocity and acceleration have the same sign, the particle is speeding up, not slowing down, and the relationship between acceleration and velocity does depend on their angle.
Final Answer
Both the assertion and reason are false.
---
The assertion states that for a particle moving along a straight line, if the velocity and acceleration have the same sign, then the particle may be slowing down.
- If both velocity and acceleration are positive, the particle is speeding up.
- If both are negative, the particle is also speeding up (in the negative direction).
- Therefore, if the velocity and acceleration have the same sign, the particle cannot be slowing down; it is actually speeding up.
The reason states that for a moving particle, speeding up and slowing down does not depend upon the angle between velocity and acceleration.
- The angle between velocity and acceleration does affect whether the particle speeds up or slows down.
- If acceleration has a component in the direction of velocity (same direction), the particle speeds up.
- If acceleration has a component opposite to the direction of velocity (opposite direction), the particle slows down.
- Thus, the statement that speeding up and slowing down does not depend on the angle is incorrect.
Both the assertion and reason are false. The correct conclusion is that if velocity and acceleration have the same sign, the particle is speeding up, not slowing down, and the relationship between acceleration and velocity does depend on their angle.
Both the assertion and reason are false.
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 3
99 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
If a particle is moving along straight line with increasing speed, then
View SolutionThe variation of velocity of a particle moving along a straight line is shown in . is
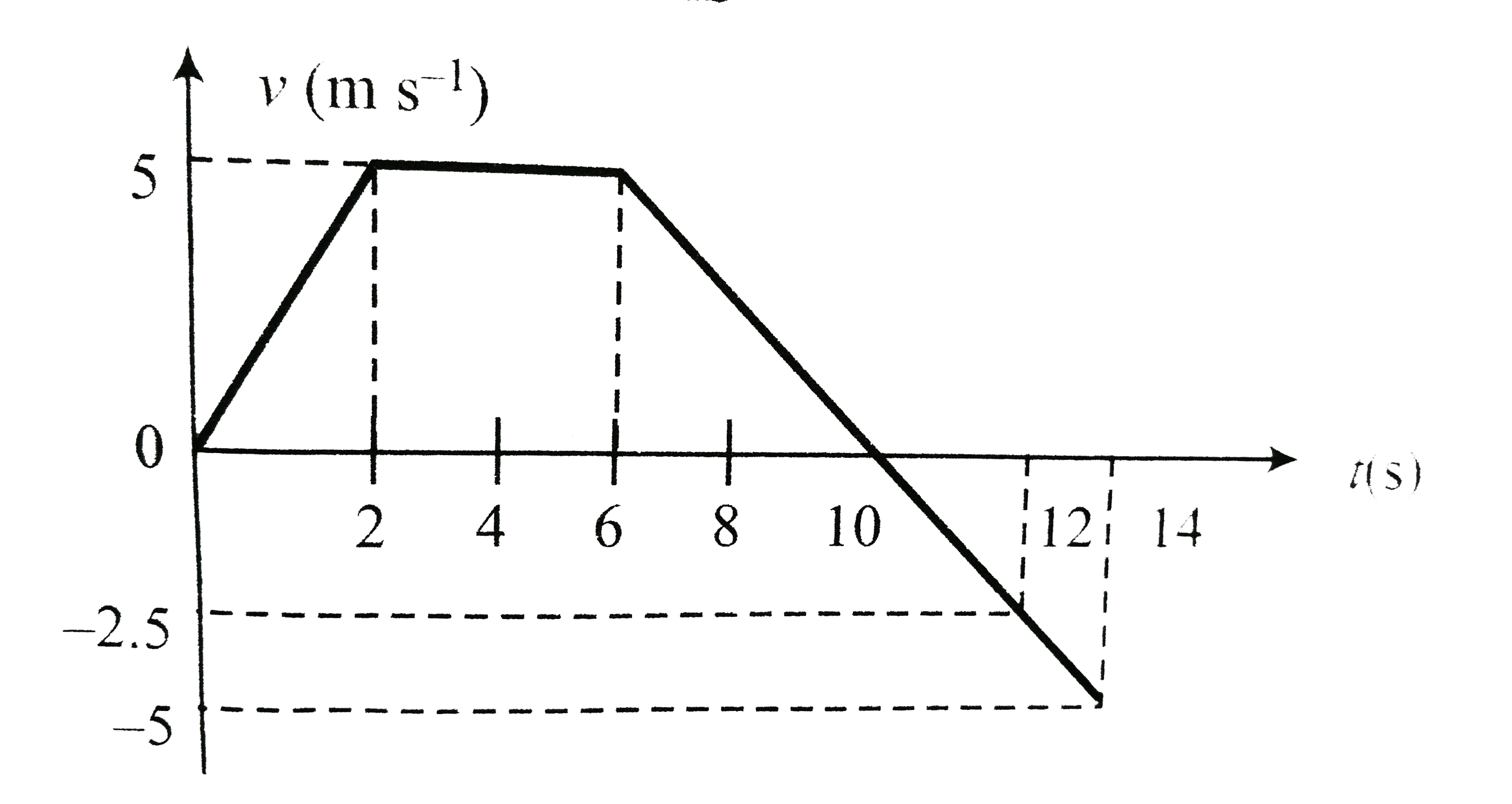 .
.
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−

View SolutionA particle moves on a straight line with a uniform velocity. It's angular momentum
View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :

View SolutionTwo particles are moving along a straight line as shown. The velocity of approach between A and B is
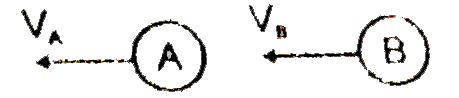
View SolutionMark the correct statements for a particle go ing on a straight line:
(a) If the velocity and acceleration have opposite sign, the object is slowing down.
(b) If the position and velocity have opposite sign, the particle is moving towards the origin.
(c) If the velocity is zero at an instant, the acceleration should also be zero at that instant.
(d) If the velocity is zero for a time interval, the acceleration is zero at any instant within the time interval.
View SolutionFor a particle moving in straight line with increasing speed the appropriate sign of acceleration a and velocity v can be:
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View Solution
