A particle of mass 2m is connected by an inextensible string of length 1.2m to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
0
0.4
0.8
1.2
The correct Answer is:C
To solve the problem, we need to determine how far the ring moves when the string becomes vertical. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
We have a particle of mass 2m hanging from a ring of mass m via an inextensible string of length 1.2 m. The system is initially at rest with the particle and the ring at the same horizontal level.
Step 2: Identify the Center of Mass (COM)
The center of mass of the system can be calculated using the formula:
xcm=m1x1+m2x2m1+m2
where:
- m1=2m (mass of the particle)
- m2=m (mass of the ring)
- x1 is the position of the particle (which we will take as 1.2 m when the string is vertical)
- x2 is the position of the ring (which we will denote as x)
Step 3: Set Up the Equation
When the string becomes vertical, the distance from the ring to the center of mass can be expressed as:
xcm=(2m)(1.2)+(m)(x)2m+m
This simplifies to:
xcm=2.4m+mx3m
xcm=2.4+x3
Step 4: Calculate the Position of the Center of Mass
Since the string is vertical, the center of mass will remain at the same horizontal position due to the absence of horizontal forces. The center of mass will be at a distance of 0.8 m from the ring when the string is vertical. Thus, we set:
xcm=0.8
Step 5: Solve for x
Now we can set up the equation:
0.8=2.4+x3
Multiplying both sides by 3:
2.4+x=2.4
Subtracting 2.4 from both sides:
x=0.8
Conclusion
The distance moved by the ring when the string becomes vertical is 0.8 m.
Final Answer
The distance moved by the ring is 0.8 m.
---
We have a particle of mass 2m hanging from a ring of mass m via an inextensible string of length 1.2 m. The system is initially at rest with the particle and the ring at the same horizontal level.
The center of mass of the system can be calculated using the formula:
xcm=m1x1+m2x2m1+m2
where:
- m1=2m (mass of the particle)
- m2=m (mass of the ring)
- x1 is the position of the particle (which we will take as 1.2 m when the string is vertical)
- x2 is the position of the ring (which we will denote as x)
When the string becomes vertical, the distance from the ring to the center of mass can be expressed as:
xcm=(2m)(1.2)+(m)(x)2m+m
This simplifies to:
xcm=2.4m+mx3m
xcm=2.4+x3
Since the string is vertical, the center of mass will remain at the same horizontal position due to the absence of horizontal forces. The center of mass will be at a distance of 0.8 m from the ring when the string is vertical. Thus, we set:
xcm=0.8
Now we can set up the equation:
0.8=2.4+x3
Multiplying both sides by 3:
2.4+x=2.4
Subtracting 2.4 from both sides:
x=0.8
The distance moved by the ring when the string becomes vertical is 0.8 m.
The distance moved by the ring is 0.8 m.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II43videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III42videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
Two particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
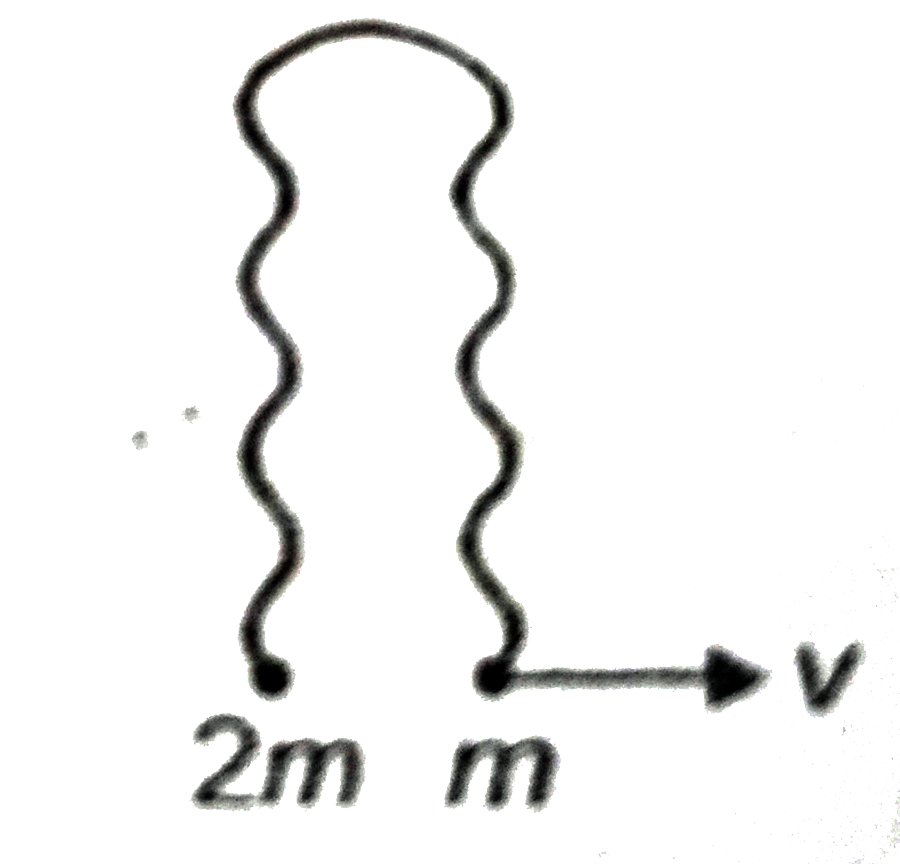 View Solution
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
 View Solution
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
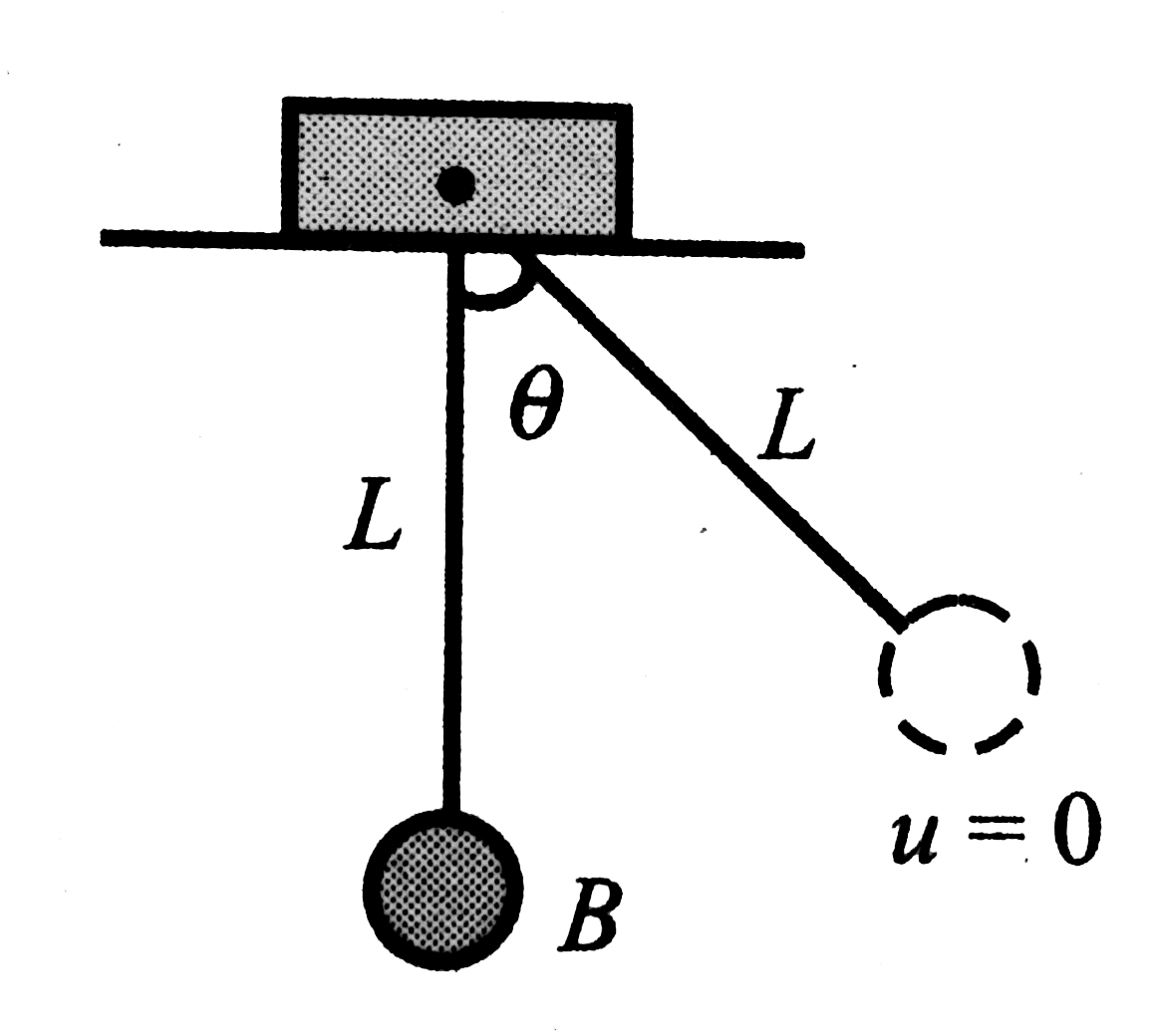 The displacement of centre of mass of A+B system till the string becomes vertical is View Solution
The displacement of centre of mass of A+B system till the string becomes vertical is View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be
 View Solution
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is
 View Solution
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA small ball of mass m is connected by an inextensible massless string of length with an another ball of mass M=4m. They are released with zero tension in the string from a height h as shown in the figure. Find the time when the string becomes taut for the first time after the mass M collides with the ground. Take all collisions to be elastic.
 View Solution
View SolutionA particle of mass m is attached to a string of length L and given velocity √10gL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (i) lowest position (ii) highest position,
View Solution

