Two identical particles of mass m carry a charge Q each. Initially one is at rest on a smooth horizontal plane and the other is projected along the plane directly towards first particle from a large distance with speed v. The closest distance of approach be :
The correct Answer is:Q2mπ∈0V2
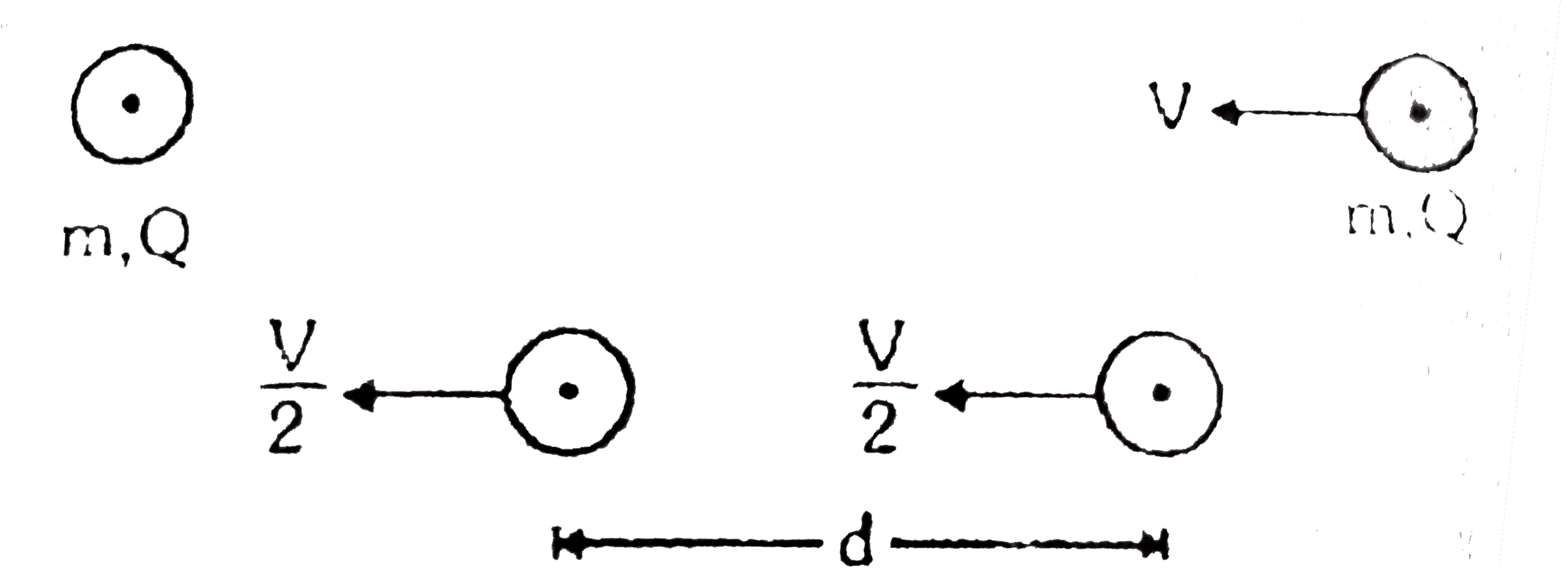
Conservation of momentum (COM)
0+mV=(m+m)Vf,Vf=V2
COME: 12mV2=12m(V2)2+12m(V2)2+Kq2d
d=Q2πm∈0v2
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exersice-04[B]
Explore 16 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-05(A)
Explore 35 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Comprehension 9
Explore 2 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
Two charged particles of masses m and 2m are placed distance d apart on a smooth horizontal table. Because of their mutual attraction, they move towards each other and collide. Where will the collision occur with respect to the initial positions?
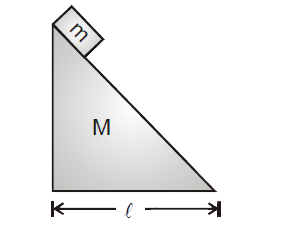
View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
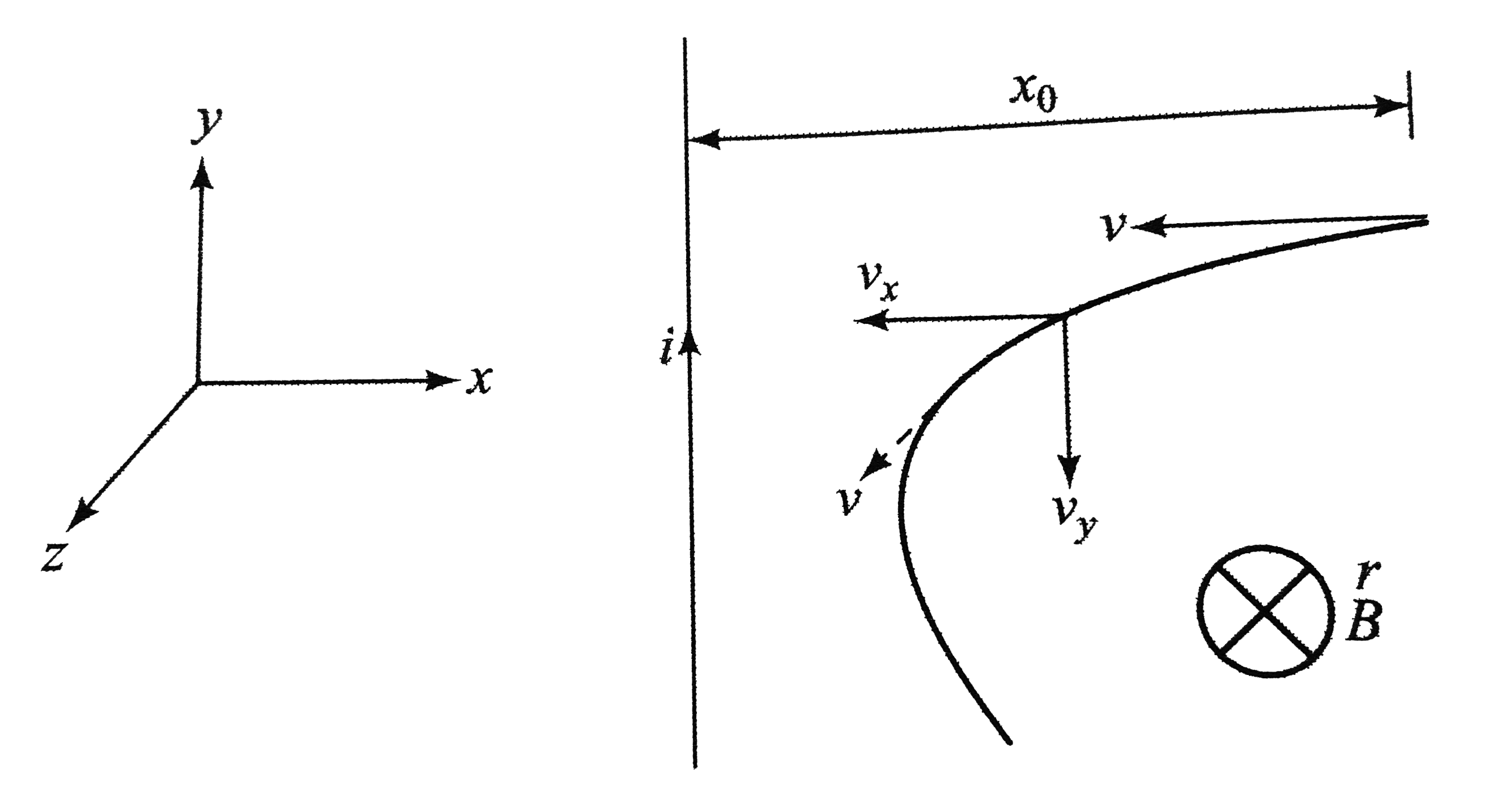
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.

View SolutionFour identical positive point charges Q are fixed at the four corners of a square of side length l. Another charged particle of mass m and charge +q is projected towards centre of square from a large distance along the line perpendicular to plane of square. The minimum value of initial velocity v0 (in m/s) required to cross the square is ?
(m=1gm,l=4√2m,Q=1μc,q=0.5μc)

View SolutionTwo blocks of masses m1 and m2 are connected by a massless pulley A, slides along th esmooth sides of a rectangular wedge of mass m, which rests on a smooth horizontal plane. Find the distance covered by the wedge on the horizontal plane till the mass m1 is lowered by the vertical distance h.
View SolutionA particle approaches from very large distance towards concave mirror along the principal axis. By the time the particle reaches the mirror the distance between the particle and its image will
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionTwo identical particles each of mass m are connected by a light spring of stiffness K. The initial deformation of the spring when the system was at rest, x0. After releasing the system, if one of the particles has a speed v and the deformation of the spring is x, find the speed of the other particle neglecting friction.
View SolutionA particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View Solution