Statement-1 : For any collision, coefficient of restitution (e lies between 0 and 1.
Statement-2 : This is because no collision may be 100% elastic or 100% inelastic.
If both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertiion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are False
The correct Answer is:A
To solve the question regarding the statements about the coefficient of restitution, we will analyze each statement step by step.
Step 1: Understanding the Coefficient of Restitution
The coefficient of restitution (denoted as e) is defined as the ratio of the relative velocity of separation to the relative velocity of approach between two colliding bodies. Mathematically, it is expressed as:
\(
e = \frac{\text{Velocity of separation}}{\text{Velocity of approach}}
\)
Step 2: Range of the Coefficient of Restitution
The value of e can range from 0 to 1:
- If e=1, the collision is perfectly elastic, meaning that kinetic energy is conserved.
- If e=0, the collision is perfectly inelastic, meaning that the two bodies stick together after the collision.
Step 3: Analyzing Statement 1
Statement 1: "For any collision, the coefficient of restitution e lies between 0 and 1."
This statement is true because, by definition, the coefficient of restitution cannot exceed 1 (perfectly elastic collision) or fall below 0 (perfectly inelastic collision).
Step 4: Analyzing Statement 2
Statement 2: "This is because no collision may be 100% elastic or 100% inelastic."
This statement is also true. In real-world scenarios, all collisions have some degree of energy loss due to factors like sound, heat, and deformation, making it impossible to achieve a perfectly elastic or perfectly inelastic collision.
Step 5: Conclusion
Both statements are true. Moreover, Statement 2 provides a valid explanation for Statement 1. Therefore, the correct conclusion is that both statements are true, and Statement 2 correctly explains Statement 1.
Final Answer
Both statements are true, and Statement 2 is the correct explanation for Statement 1.
---
The coefficient of restitution (denoted as e) is defined as the ratio of the relative velocity of separation to the relative velocity of approach between two colliding bodies. Mathematically, it is expressed as:
e = \frac{\text{Velocity of separation}}{\text{Velocity of approach}}
\)
The value of e can range from 0 to 1:
- If e=1, the collision is perfectly elastic, meaning that kinetic energy is conserved.
- If e=0, the collision is perfectly inelastic, meaning that the two bodies stick together after the collision.
Statement 1: "For any collision, the coefficient of restitution e lies between 0 and 1."
This statement is true because, by definition, the coefficient of restitution cannot exceed 1 (perfectly elastic collision) or fall below 0 (perfectly inelastic collision).
Statement 2: "This is because no collision may be 100% elastic or 100% inelastic."
This statement is also true. In real-world scenarios, all collisions have some degree of energy loss due to factors like sound, heat, and deformation, making it impossible to achieve a perfectly elastic or perfectly inelastic collision.
Both statements are true. Moreover, Statement 2 provides a valid explanation for Statement 1. Therefore, the correct conclusion is that both statements are true, and Statement 2 correctly explains Statement 1.
Both statements are true, and Statement 2 is the correct explanation for Statement 1.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
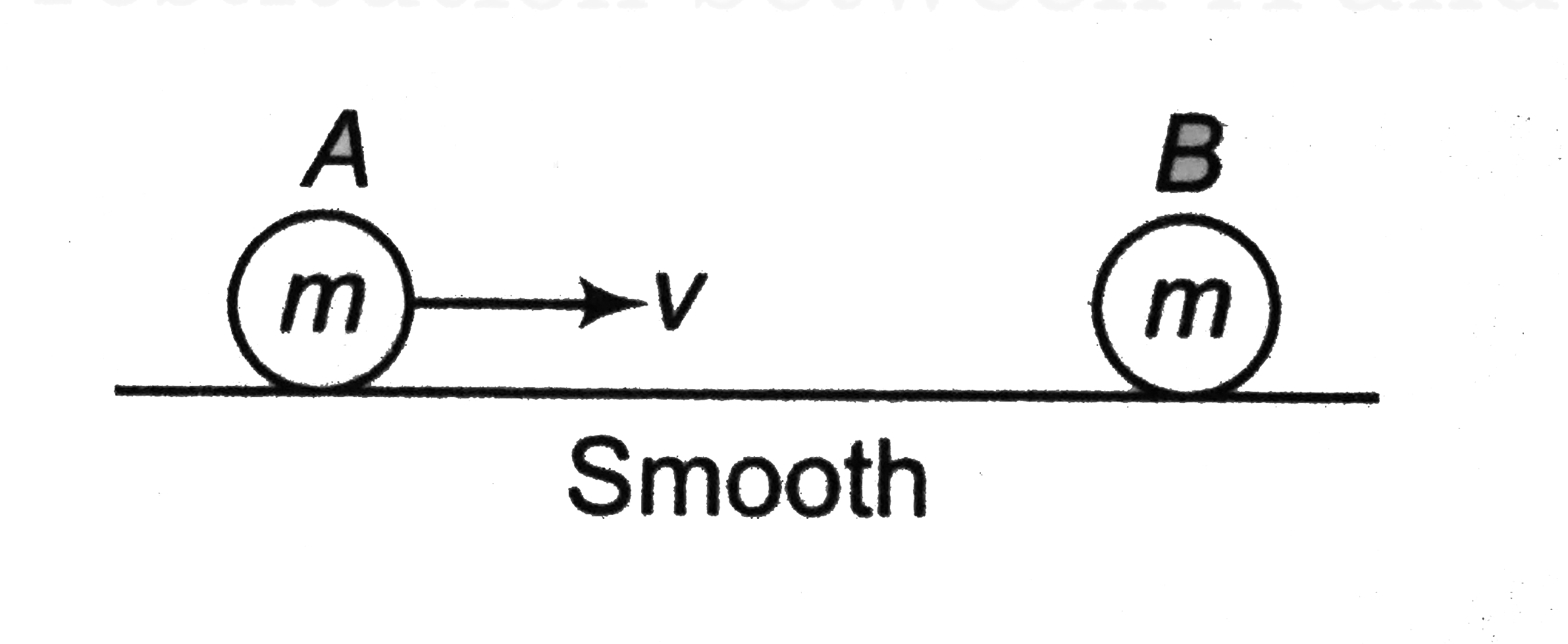
In the figure shown, coefficient of restitution between A and B is e=12, then
View SolutionThe coefficient of restitution e for a perfectly elastic collision is
View SolutionStatement-1 : In an elastic collision in one dimension between two bodies, total momentum remains the same before, during and after the collision.
Statement-2 : In an elastic collision in one dimension between two bodies, total kinetic energy remains the same before, during and after the collision.
View SolutionStatement-1 : The coefficient of restitution is less than one for all collision studied under Newton's laws of restituation.
and
Statement-2 : For a perfeclty elastic collision, coefficient of restitution is equal to one .
View SolutionThe cofficient of restitution e for a perfectly elastic collision is
(a) 1 (b) zero (c) infinite (d) -1
View SolutionA ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
View SolutionTwo balls of masses m and 2m and momenta 4p and 2p (in the directions shown) collide as shown in figure. During collsion, the value of linear impulse between them is J. In terms of J and p find coefficient of restitution 'e'. Under what condition collision is elastic. Also find the condition of perfectly inelastic collision.

View SolutionA ball stikes a horizontal floor at an angle theta = 30° with normal to the floor . The coefficient of restitution between the ball and floor is. e=13. The percentage of its kinetic energy lost in the collision is nearly
View SolutionThree identical balls, ball I, ball II and ball III are placed on a smooth floor on a straight line at the separation of 10m between balls as shown in figure. Initially balls are stationary. But I is given velocity of 10m/s towards ball II, collision between balls I and II is inelastic with coefficient of restitution 0.5 but collision between balls II and III is perfectly elastic. What is the time interval between two consecutive collisions between ball I and II?

View SolutionThree identical balls, ball I, ball II and ball III are placed on a smooth floor on a straight line at the separation of 10m between balls as shown in figure. Initially balls are stationary. But I is given velocity of 10m/s towards ball II, collision between balls I and II is inelastic with coefficient of restitution 0.5 but collision between balls II and III is perfectly elastic. What is the time interval between two consecutive collisions between ball I and II?

View Solution
