The average velocity of a particle moving on a straight line is zero in a time interval.
Assertion :− It is possible that the instantaneous acceleration is never zero in the interval.
Reason :− It is possible that the instantaneous velocity is never zero in the interval.
If both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertiion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are False
The correct Answer is:C
To solve the question, we need to analyze the given assertion and reason in the context of motion.
1. Understanding Average Velocity:
- Average velocity (Vavg) is defined as the total displacement divided by the total time taken.
- If the average velocity is zero over a time interval, it implies that the initial and final positions of the particle are the same.
2. Analyzing the Assertion:
- The assertion states that it is possible for the instantaneous acceleration to never be zero during the interval.
- Instantaneous acceleration is defined as the rate of change of velocity at a particular instant.
- Even if the average velocity is zero, the particle can still be accelerating (changing its velocity) throughout the interval. For example, a particle could move back and forth, changing its speed and direction, while returning to the same position. Thus, the assertion is true.
3. Analyzing the Reason:
- The reason states that it is possible for the instantaneous velocity to never be zero in the interval.
- Instantaneous velocity is the velocity of the particle at a specific instant. If the particle moves from point A to point B and back to A, there will be moments when the particle is at rest (velocity = 0) when it changes direction.
- Therefore, it is not possible for the instantaneous velocity to never be zero if the particle returns to the same position. Thus, the reason is false.
4. Conclusion:
- Since the assertion is true and the reason is false, the correct answer is that the assertion is true and the reason is false.
Final Answer:
- Assertion: True
- Reason: False
- Therefore, the answer is option C.
- Average velocity (Vavg) is defined as the total displacement divided by the total time taken.
- If the average velocity is zero over a time interval, it implies that the initial and final positions of the particle are the same.
- The assertion states that it is possible for the instantaneous acceleration to never be zero during the interval.
- Instantaneous acceleration is defined as the rate of change of velocity at a particular instant.
- Even if the average velocity is zero, the particle can still be accelerating (changing its velocity) throughout the interval. For example, a particle could move back and forth, changing its speed and direction, while returning to the same position. Thus, the assertion is true.
- The reason states that it is possible for the instantaneous velocity to never be zero in the interval.
- Instantaneous velocity is the velocity of the particle at a specific instant. If the particle moves from point A to point B and back to A, there will be moments when the particle is at rest (velocity = 0) when it changes direction.
- Therefore, it is not possible for the instantaneous velocity to never be zero if the particle returns to the same position. Thus, the reason is false.
- Since the assertion is true and the reason is false, the correct answer is that the assertion is true and the reason is false.
- Assertion: True
- Reason: False
- Therefore, the answer is option C.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
If average velocity of particle moving on a straight line is zero in a time interval, then
View SolutionAssertion: The average velocity of a particle is zero in a time interval. It is possible that the instantaneous acceleration is never zero in the interval.
Reason: The magnitude of average velocity in an interval is equal to its average speed in that interval.
View SolutionThe velocity of a particle is zero at time t = 2s, then
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionAssertion: When a particle moves with constant velocity its average velocity, its insttantaneous velocity and its speed are all equal in magnitude.
Reason: If the average velocity of a particle moving on a straight line is zero in a time interval, then it is possible that the instantaneous velocity is never zero in the internal.
View SolutionThe figure below shows the velocity-time graph of a body moving in a straight line.
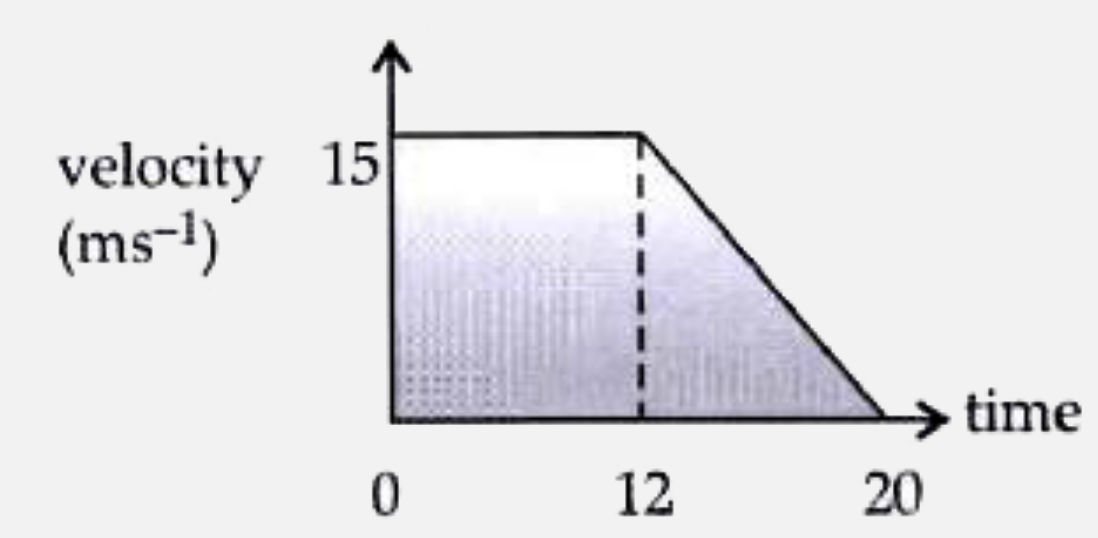
Find the time interval in which the body is moving with zero acceleration
View SolutionFor which of the following graphs the average velocity of a particle moving along a straight line for time interval (0,t) must be negative−
View SolutionFor which of the following graphs the average velocity of a particl moving along a straight line for time interval (0,t) must be negative−
View SolutionThe instantaneous velocity of a particle is equal to time derivative of its position vector and the instantaneous acceleration is equal to time derivatives of its velocity vector. Therefore :
View Solution
